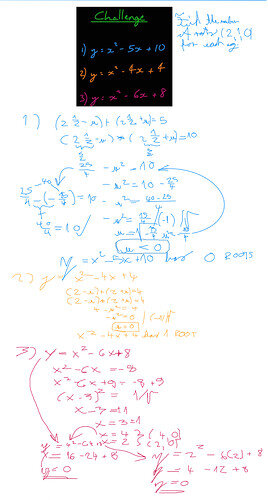More and more challenging! 
y = x^2 - 5x + 10
(-5/2 - u)(-5/2 + u) = 10
25/4 - u^2 = 10
u^2 = 25/4 - 10 = (25 - 40)/4 = - 15/4
u = sqrt(- 15/4)
=> Zero roots
y = x^2 - 4x + 4
(-2 - u)(-2 + u) = 4
4 - u^2 = 4
u^2 = 0
u = 0
=> One root (x = 0)
y = x^2 - 6x + 8
(-3 - u)(-3 + u) = 8
9 - u^2 = 8
u^2 = 9 - 8 = 1
u = sqrt(1) = 1
=> Two roots (x = -4, x = -2)
@Carl_Gustafsson, you’re close but you’ve made a similar mistake each time which has lead to the wrong locations for your roots.
When you half b you also want to flip the signs.
So for the first one it’s (5/2 + u)(5/2 - u) = 10, the second is (2 + u)(2 - u) = 4 and lastly (3 + u)(3 - u) = 8.
So once you’ve got an answer for u you can plug that back in and get the correct results of:
Oh. Thanks!
How silly of me - I missed that I should have changed the sign. If I had been really thorough I would of course have converted back and seen whether it returned the same equation as the initial one or not.
Don’t worry, it happens to the best of us! 
What is maths for video games course about?
1). y=x^2−5x+10
((5/2)+u)((5/2)−u)=10
(25/4)−u^2=10
−u^2=(40/4)−(25/4)
u^2=−(15/4)
No root
2). y=x^2−4x+4
(2+u)(2−u)=4
4−u^2=4
u^2=0
(2+0)(2-0)=4
y=(x−2)^2
1 intercept @ (2, 0)
3.) y=x^2−6x+8
(3+u)(3−u)=8
9−u^2=8
u^2=1
u=1
(3+1)(3−1)=8
(4)∗(2)=8
y=(x−2)(x−4)
2 intercepts @ (2, 0), (4, 0)
Equation 1: no root
Equation 2: 1 root
Equation 3: 2 roots[
1) 0 root
2) 1 root
3) 2 roots
My results:
y = x² - 5x + 10
(3 - u)(3 + u) = 10
9 - u² = 10
u² = -1
0 roots
y = x² - 4x + 4
(2 - u)(2 + u) = 4
4 - u² = 4
u² = 0
1 root
y = x² - 6x + 8
(3 - u)(3 + u) = 8
9 - u² = 8
u² = √1
u = 1
2 roots
y = x^2 -5x + 10 has no roots
y = x^2 -4x + 4 has one root
y = x^2 -6x + 8 has 2 roots
1) no root
2) one root
3) two roots
Here goes:
1 has no root
2 has 1 root
3 has 2 roots -1 and 1
1. y = x^2 - 5x + 10
(u+2.5)(u-2.5) = 10
6.25 - u^2 = 10
u^2 = -3.75Answer: 0 roots
2. y = x^2 - 4x + 4
(u+2)(u-2) = 4
4 - u^2 = 4
u^2 = 0Answer: 1 roots
3. y = x^2 - 6x + 8
(u+3)(u-3) = 8
9 - u^2 = 8
u^2 = 1Answer: 2 roots
I struggled a bit with the last one tbh. I dropped a comment on the video, where I asked you to clarify a specific thing you said in the video. @garypettie
Thanks.
Hi @jengberg, I can’t see your comment on the video.
If you let me know what where you are struggling I’d be happy to help.
Hi Gary! No worries. You have already replied to my comment on the video and now I have better understanding this. Thanks
The last is solved with compleeting the square that is adding a (6/2) on 2 to get a 9 to both sides of the equation and so getting the x = 4 and x = 2. By testing theese values back into the equation you get y = 0 that is certainly the x intercept at 4 and 2. That is root 1 at (4. 0) and root 2 at (2, 0).
Cheers
y = x^2 -5x +10
(5/2 + u)(5/2 - u) = 10
25/4 - u^2 = 10
u^2 = 25/4 - 40/4
u^2 = -15/4
u = square root of -3.75
This is an imaginary number so it has zero roots.
y = x^2 - 4x + 4
(2 + u)(2 - u) = 4
4 - u^2 = 4
u^2 = 0
u = 0
2 x 2 = 4
2 + 2 = 4
One root
(2,0)
3.y = x^2 - 6x +8
(3 + u)(3 - u) = 8
9 - u^2 = 8
u^2 = 1
u = 1
4 x 2 = 8
4 + 2 = 6
Two roots.
(2,0)(4,0)
