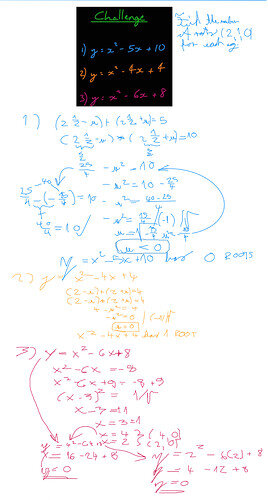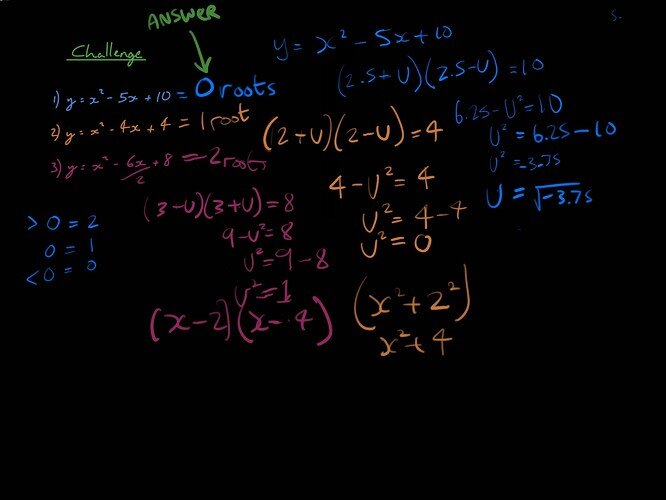Hi @jengberg, I can’t see your comment on the video.
If you let me know what where you are struggling I’d be happy to help.
Hi Gary! No worries. You have already replied to my comment on the video and now I have better understanding this. Thanks 
The last is solved with compleeting the square that is adding a (6/2) on 2 to get a 9 to both sides of the equation and so getting the x = 4 and x = 2. By testing theese values back into the equation you get y = 0 that is certainly the x intercept at 4 and 2. That is root 1 at (4. 0) and root 2 at (2, 0).
Cheers
-
y = x^2 -5x +10
(5/2 + u)(5/2 - u) = 10
25/4 - u^2 = 10
u^2 = 25/4 - 40/4
u^2 = -15/4
u = square root of -3.75
This is an imaginary number so it has zero roots. -
y = x^2 - 4x + 4
(2 + u)(2 - u) = 4
4 - u^2 = 4
u^2 = 0
u = 0
2 x 2 = 4
2 + 2 = 4
One root
(2,0)
3.y = x^2 - 6x +8
(3 + u)(3 - u) = 8
9 - u^2 = 8
u^2 = 1
u = 1
4 x 2 = 8
4 + 2 = 6
Two roots.
(2,0)(4,0)
Ok here we go!
- y = x^2 - 5x + 10
(5/2 + u)(5/2 - u) = 10
25/4 - u^2 = 10
u^2 = -40/4 - 25/4 = -65/4
u is imaginary so there are 0 roots
- y = x^2 - 4x + 4
(2+u)(2-u) = 4
4 - u^2 = 4
u^2 = 0
parabola has one root
y = (x-2)^2 - root is at (2,0)
- y = x^2 - 6x + 8
(3+u)(3-u) = 8
9 - u^2 = 8
u^2 = 1
u = 1
parabola has 2 roots
y = (x-2)(x-4)
therefore roots are at (2,0) and (4,0)
i get
1 has 2 roots
2 has 1 root
and 3 has 0 roots.
1)no roots ((5/2-u)(5/2+u)=10 => u^2=25/4-10=(25-40)/2=-7.5)
2)1 root ((2-u)(2+u)=4 => u^2=0)
3)2 roots ((3-u)(3+u)=8 => u^2=1)
-
y = x^2 - 5x + 10
(5/2 - u) * (5/2 + u) = 10
25/4 - u^2 = 10
u^2 = -15/4
u = √-15/4
No rutes -
y = x^2 - 4x + 4
(2 - u) * (2 + u) = 4
4 - u^2 = 4
u^2 = 0
u = 0
1 root -
y = x^2 - 6x + 8
(3 - u) (3 + u) = 8
9 - u^2 = 8
u^2 = 1
u = 1
2 roots
-
y = x² - 5x + 10
(5/2 + u)(5/2 - u) = 10
25/4 - u² = 10
u ²= -15/4
u = √-15/4
This is an imaginary number, So the equation has no root -
y = x² - 4x + 4
(2 + u)(2 - u) = 4
4 - u² = 4
u ²= 0
u = 0
(2 + 0)(2 - 0) = 4y = (x + 2)²
This equation has one root (2, 0) -
y = x² - 6x + 8
(3 + u)(3 - u) = 8
9 - u² = 8
u ²= 1
u = 1
(3 + 1)(3 - 1) = 8
4 * 2 = 8y = (x + 2)(x + 4)
This equation has two roots (2, 0) and (4, 0)
Challenges:
(FOIL)
1.) y = x^2 - 5x + 10
(2.5 + u)(2.5 - u) = 10
2.5 * 2.5 = 6.25
2.5 * -u = -2.5u
u * 2.5 = 2.5u
u * -u = -u^2
6.25 - u^2 = 10
u^2 = 6.25 - 10
u^2 = -3.75
[Challenge 1 has 0 roots.]
2.) y = x^2 - 4x + 4
(2 + u)(2 - u) = 4
2 * 2 = 4
2 * -u = -2u
u * 2 = 2u
u * -u = -u^2
4 - u^2 = 4
u^2 = 4-4
u^2 = 0
u = sqr(0)
u = 0
[Challenge 2 has 1 root.]
3.) y = x^2 - 6x + 8
(3 + u)(3 - u) = 8
3 * 3 = 9
3 * -u = -3u
u * 3 = 3u
u * -u = -u^2
9 - u^2 = 8
u^2 = 9-8
u^2 = 1
u = 1
[Challenge 3 has 2 roots.]
Here’s my answers for the Less Than Two Roots challenge:
Q. Given the three equations below, decide which has no root, one root, and two roots.
Q1. y = x² - 5x + 10
A1. This equation has no roots
A1a. In all honesty, I figured this one pretty quickly because starting off by doing 5/2 made me highly suspicious, so I just stopped there and did the others first.
Q2. y = x² - 4x + 4
A2. This equation has one root.
A2a. (2 + u)(2 - u) = 4
A2b. 4 - u² = 4
A2c. -u² = 0
A2d. u = 0
A2e. (2 + 0)(2 - 0) = 4
A2f. 2 * 2 = 4
A2g. Our intercept values are the same: (2, 0) and (2, 0), therefore we only have one intercept (we also knew this from our 0-value for u earlier).
Q3. y = x² - 6x + 8
A3. This equation has two roots.
A3a. (3 + u)(3 - u) = 8
A3b. 9 - u² = 8
A3c. -u² = -1
A3d. u² = 1
A3e. u = 1
A3f. (3 + 1)(3 - 1) = 8
A3g. 4 * 2 = 8
A3h. Our two intercepts are (2, 0) and (4, 0)
Good challenge. I messed up on the 2nd one and got a strange answer, then checked here to find my error.
- y = x^2 - 5x + 10
I end up with sqrt of -3.75: 0 roots
- y = x^2 - 4x + 4 =>
u = 0. So y = (x - 2)^2 and has only 1 intercept at (2,0)
- y = x^2 - 6x + 8 =>
y = (x - 4)(x - 2) so 2 roots at (4,0) (2,0)