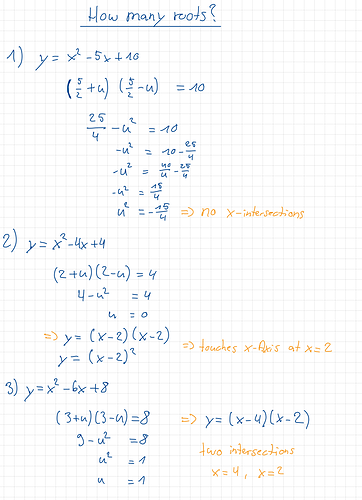Math - Less than Two Roots - Challenge

[garypettie]

In this lecture we looked at quadratic equations that have less than two roots and found a quick way of checking this using the method we learnt in the previous lecture.

For your challenge, take the following 3 equations and work out how many roots they have;

1. y = x^2 - 5x + 10
2. y = x^2 - 4x + 4
3. y = x^2 - 6x + 8

Post your answer below and remember to use spoiler tags.

[Donlod]

[ProvencalG]

1. y = x² - 5x + 10
   (2.5 + u)(2.5 - u) = 10
   6.25 - u² = 10
   u² = 6.25 - 10
   u = √-3.75
   This is an imaginary number, so the curve of the equation has no root.

2. y = x² - 4x + 4
   (2 + u)(2 - u) = 4
   4 - u² = 4
   u² = 4 - 4
   u = 0
   That means that the curve of this equation has 1 root, of (2,0).

3. y = x² - 6x + 8
   (3 + u)(3 - u) = 8
   9 - u² = 8
   u² = 9 - 8
   u = 1
   That means that the curve of this equation has 2 roots of (2,0) and (4,0).

[olidadda]

1. u^2 = 25/4 - 40/4 It’s going to be negative so no roots
2. u^2 = 0 so one root at (2,0)
3. y = (x-2)(x-4), roots at (2,0) and (4,0)

[Ajai_Raj]

1. I got to u = the square root of -15/4 = Zero roots
2. u = 0 = One root
3. u = 1 = 2 roots

[Carl_Gustafsson]

More and more challenging!

1. y = x^2 - 5x + 10
   (-5/2 - u)(-5/2 + u) = 10
   25/4 - u^2 = 10
   u^2 = 25/4 - 10 = (25 - 40)/4 = - 15/4
   u = sqrt(- 15/4)
   => Zero roots

2. y = x^2 - 4x + 4
   (-2 - u)(-2 + u) = 4
   4 - u^2 = 4
   u^2 = 0
   u = 0
   => One root (x = 0)

3. y = x^2 - 6x + 8
   (-3 - u)(-3 + u) = 8
   9 - u^2 = 8
   u^2 = 9 - 8 = 1
   u = sqrt(1) = 1
   => Two roots (x = -4, x = -2)

[garypettie]

@Carl_Gustafsson, you’re close but you’ve made a similar mistake each time which has lead to the wrong locations for your roots.

When you half b you also want to flip the signs.
So for the first one it’s (5/2 + u)(5/2 - u) = 10, the second is (2 + u)(2 - u) = 4 and lastly (3 + u)(3 - u) = 8.

So once you’ve got an answer for u you can plug that back in and get the correct results of:

1. No roots
2. One root at (2,0)
3. Two roots at (2,0) and (4,0)

[Carl_Gustafsson]

Oh. Thanks!
How silly of me - I missed that I should have changed the sign. If I had been really thorough I would of course have converted back and seen whether it returned the same equation as the initial one or not.

[garypettie]

Don’t worry, it happens to the best of us!

[kaushal_vetsa]

What is maths for video games course about?

[Nina]

Hi Kaushal,

I’ve already replied in your other thread.

[Dendrolis]

1). y=x^2−5x+10
((5/2)+u)((5/2)−u)=10
(25/4)−u^2=10
−u^2=(40/4)−(25/4)
u^2=−(15/4)
No root

2). y=x^2−4x+4
(2+u)(2−u)=4
4−u^2=4
u^2=0
(2+0)(2-0)=4
y=(x−2)^2
1 intercept @ (2, 0)

3.) y=x^2−6x+8
(3+u)(3−u)=8
9−u^2=8
u^2=1
u=1
(3+1)(3−1)=8
(4)∗(2)=8
y=(x−2)(x−4)
2 intercepts @ (2, 0), (4, 0)

[Joshzerogod]

Equation 1: no root
Equation 2: 1 root
Equation 3: 2 roots[

[DefectiveButCaring]

1) 0 root
2) 1 root
3) 2 roots

[TheSnooze]

My results:

1. y = x² - 5x + 10
   (3 - u)(3 + u) = 10
   9 - u² = 10
   u² = -1
   0 roots

2. y = x² - 4x + 4
   (2 - u)(2 + u) = 4
   4 - u² = 4
   u² = 0
   1 root

3. y = x² - 6x + 8
   (3 - u)(3 + u) = 8
   9 - u² = 8
   u² = √1
   u = 1
   2 roots

[Kbot]

y = x^2 -5x + 10 has no roots
y = x^2 -4x + 4 has one root
y = x^2 -6x + 8 has 2 roots

[u571989]

1. 0 roots
2. 1 root
3. 2 roots

[Gianni]

1) no root
2) one root
3) two roots

[Manie_Besselaar]

Here goes:

1 has no root
2 has 1 root
3 has 2 roots -1 and 1

[jengberg]

1. y = x^2 - 5x + 10

(u+2.5)(u-2.5) = 10
6.25 - u^2 = 10
u^2 = -3.75

Answer: 0 roots

2. y = x^2 - 4x + 4

(u+2)(u-2) = 4
4 - u^2 = 4
u^2 = 0

Answer: 1 roots

3. y = x^2 - 6x + 8
(u+3)(u-3) = 8
9 - u^2 = 8
u^2 = 1

Answer: 2 roots

I struggled a bit with the last one tbh. I dropped a comment on the video, where I asked you to clarify a specific thing you said in the video. @garypettie

Thanks.