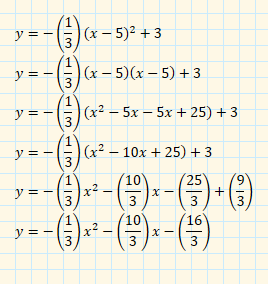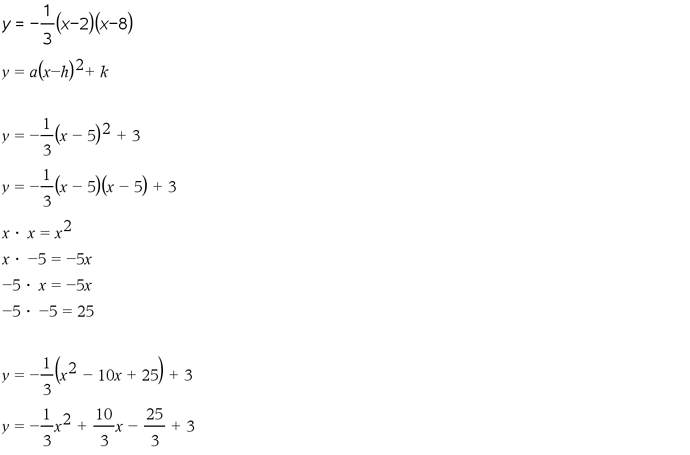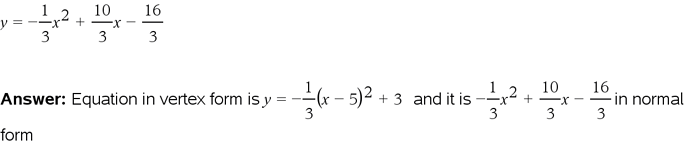Math - Vertex Form

[garypettie]

In this lecture we were introduced to the vertex form, or squared form, of the quadratic equation.

This form is incredibly useful for quickly seeing where the vertex of the parabola is - hence it’s name.

For your challenge, find the equation in vertex form for the curve that runs through the points (2,0), (5,3), and (8,0).

In intercept form, this was y = -1/3(x - 2)(x - 8)

Remember that the answer will be in the form; y = a(x - h)^2 + k.

For a hint: You can take the ‘a’ from the other form of the equation.

Post your answers below and remember to use spoiler tags.

[Donlod]

[ProvencalG]

y = a (x - h)² + k

since a = -(1/3)
h is the vertex x, so 5.
k is the vertex y, so 3.

y = -(1/3) (x - 5)² + 3

and to verify

y = -(1/3) (x - 5)(x - 5) + 3
y = -(1/3) (x² -10x + 25) +3
y = -(1/3)x² + (10/3)x - (25/3) + (9/3)
y = -(1/3)x² + (10/3)x - (16/3)

[Ajai_Raj]

I got:

y = -1/3(x-5) + 3

Which converted back to standard form is

y = -1/3x + 10/3x - 16/3

[garypettie]

@Ajai_Raj, you forgot to square the (x-5) but other than that you’re spot on

[Dendrolis]

y=−(1/3) (x−5)^2+3
y=−(1/3)(x−5)(x−5)+3
y=−(1/3)(x^2−5x−5x+25)+3
y=−(1/3)(x^2−10x+25)+3
y=−(1/3) x^2−(10/3)x−(25/3)+(9/3)
y=−(1/3) x^2−(10/3)x−(16/3)

For context this is what it looks like in onenote (which I’m pasting from) - the formatting doesn’t seem to come over.

[KhaledAhmedYounes]

It took me a while to get right because I added the constant k before dividing (x-h)² by a

[DefectiveButCaring]

y = a(x-h)^2 + k
vertex form
y = (-1/3)(x - 5)^2 + 3
then making the proof by putting it in standard form
y = (-1/3)(x - 5)(x - 5) + 3
y = (-1/3)(x^2 -5x -5x + 25) + 3
y = (-1/3)(x^2) + (10x/3) - (25/3) + 3
there we go
y = (-1/3)(x^2) + (10x/3) - (16/3)

[jamesnash16]

I got:

y = -⅓( x - 5 )² + 3

then:

y = -⅓( 𝑥 - 5 )( 𝑥 - 5 ) + 3
y = -⅓( 𝑥² - 10𝑥 + 25 ) + 3
y = -⅓𝑥² + (10/3)𝑥 - (16/3)

[zircher]

Just for fun, for Vertex Form I think of h as ‘hex’ and k and ‘key’ since that bundles the x with h and the y with the k. So, the mnemonic goes, “Use the hex key to unlock the Vertex Form.”

[garypettie]

That’s a great mnemonic!
I’d just make the slight adjustment to “Use a hex key to unlock the Vertex Form” to capture that leading a term as well

[TheSnooze]

The vertex form would be:

y = -1/3(x - 5)² + 3

back to standard form:

y = -1/3(x - 5)(x - 5) + 3
y = -1/3(x² - 10x + 25) + 3
y = -1/3x² + 10/3x - 25/3 + 9/3
y = -1/3x² + 10/3x - 16/3

checkmate!

[Kbot]

Vertex Form: y = -1/3 (x-5)^2 + 3

-1/3 (x-5) (x-5) + 3
-1/3 (x^2 - 10x + 25) + 3
-1/3x^2 + 10/3x - 25/3 + 9/3

Standard Form: -1/3x^2 + 10/3x - 16/3

[Mikapo]

My respond:

[u571989]

the vertex formula is y=(-1/3)(x-5)^2+3

the converted to standard y=(-1/3)x^2+(10/3)-(-16/3)

[garypettie]

@u571989, it looks like you’ve missed off the x on the second term again.
The sign of the third term is also incorrect: -(-16/3) is the same as +16/3. However, that last term should be -16/3

[Manie_Besselaar]

I have

y = -1/3(x -5 )^2 + 3

which converted to
y = -1/3x^2 - 10/3x + 34/3 correction!!!
I forgot to multiply the negative for my 25 sooooo…
y = -1/3x^2 +10/3x -16/3

[hlais]

i made the same mistake, I thought the previous example followed that process too.

[jengberg]

Answer:

y = -1/3 (x - 5)^2 + 3

How to go to standard form:

y = -1/3 (x - 5) * (x-5) + 3
y = -1/3 (x^2 - 5x - 5x ) + 3
y = -1/3 (x^2 - 10x + 25) + 3
y = -1/3^2 + 10/3x - 16/3

[Dangermau5]

The answer I got was the below - second-guessed it a little bit, but it worked so I guess I need to be more confident!

y = -1/3(x-5)^2 + 3