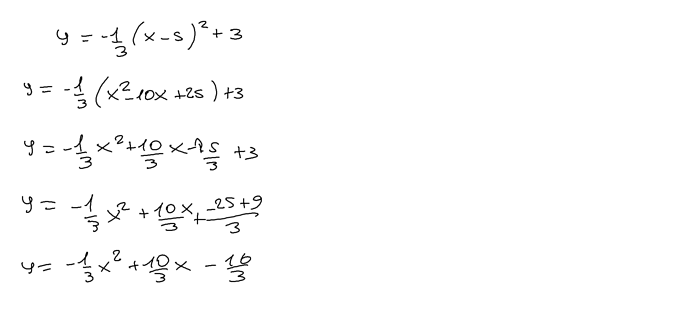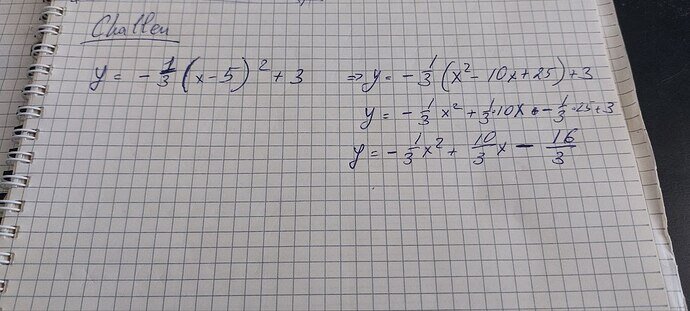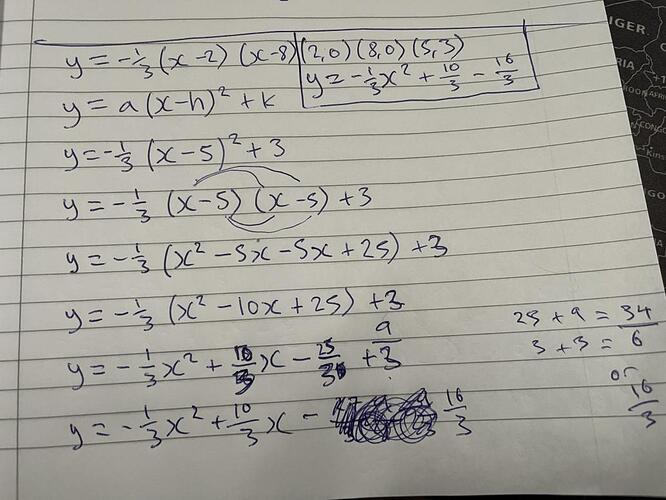Here are my steps-
y = - 1/3 (x - 5)^2 + 3
y = - 1/3 (x - 5) (x - 5) + 3
y = - 1/3 (x^2 - 5x - 5x + 25) + 3
y = - 1/3x^2 + 10/3x - 25/3 + 3
y = - 1/3x^2 + 10/3x - 16/3
I just realized that I was solving challenges on my sheet but not participating in the comment’s section so reckon I should do it. I’ll try to do this with every challenge.
Hello again my friends!
Here is “my” solution:
Standard form [ y = - 1/3x^2 + 10/3x - 16/3 ]
Cheers!
y=-(1/3)*(x-5)^2+3
y = -1/3 * (x - 5)^2 + 3
y = -1/3 * (x - 5) * (x - 5) + 3
y = -1/3 * (x^2 - 5x - 5x + 25) + 3
y = -1/3 * (x^2 -10x + 25) + 3
y = -1/3 x^2 + 10/3 x - 25/3 + 3
y = 1/3 x^2 + 10/3 x - 16/3
y = -1/3 (x - h)^2 + k
y = -1/3 (x - h)(x -h) + k
y = -1/3 (x - 5)(x - 5) + 3
y = -1/3 (x^2 - 5x - 5x + 25) + 3
y = -1/3 (x^2 - 10x + 25) + 3
y = -1/3x^2 + 10/3x - 25/3 + 3
y = -1/3x^2 + 10/3x - 16/3
Challenge:
y = (-1/3)(x-5)^2 + 3
Worked to Standard:
y = (-1/3)(x-5)(x-5)+3
FOIL:
(x-5)(x-5)
x * x = x^2
x * (-5) = -5x
(-5) * x = -5x
(-5) * (-5) = 25
x^2 - 10x + 25
y = (-1/3)(x^2 - 10x + 25) + 3
y = (-1/3)x^2 + (10/3)x - (25/3) + 3
y = (-1/3)x^2 + (10/3)x - (25/3) + (9/3)
y = (-1/3)x^2 + (10/3)x - (16/3)
I’ve got just a minor question regarding the Vertex Form challenge, but here’s my answer:
Q1. Given y = (-1/3)(x - 2)(x - 8) and a vertex of (5, 3), write the Vertex Form
A1. y = (-1/3)(x - 5)² + 3
A1a. y = (-1/3)(x - 5)(x - 5) + 3
A1b. y = (-1/3)(x² - 5x - 5x + 25) + 3
A1c. y = (-1/3)(x² - 10x + 25) + 3
A1d. y = (-1/3)x² - (10/3)x - (25/3) + 3
A1e. y = (-1/3)x² - (10/3)x - (25/3) + (9/3)
A1f. y = (-1/3)x² - (10/3)x - (16/3)
My question:
I kept on messing up when I would get to steps 1b - 1e. For the constant value at the end, I kept on adding it to the 25 which (obviously) gave me the wrong answer. Is it correct, then, for those steps to be interpreted as the following (hidden for spoilers):
y = ((-1/3)(x² - 5x - 5x + 25)) + 3
y = ((-1/3)(x² - 10x + 25)) + 3
y = (-1/3)x² + (10/3)x - (25/3) + 3
etc. …
I’ve added extra parentheses to hopefully show where my head is at… If I need to clarify further I’d be more than happy to! I feel like ultimately I’m getting hung up by not seeing the (x - 5)(x - 5) = (x² - 10x + 25) as it’s own discrete quantity that needs to remain isolated until the value of a is multiplied across, but I just want to be sure I’m checking myself correctly before getting much farther.
Struggled a bit at the end as I forgot to turn the +3 into 9/3 but got there in the end.
Do feel like I understand this more than I did processing linear equations.
Vertex form:
y = -1/3(x - 5)^2 + 3
Converted back to standard form I got:
y = -(1/3)x^2 + (10/3)x - (16/3)
To verify all of this, we can work it out with the vertex point (5,3) and find that 3 = 9/3 = 3. Yay!
I just want to say you are a fantastic teacher, it is easy to understand so far with those practical and gaming related implementations. I was not bad at maths, but i feel i have understand more in this short lessons about algebra than in a full course in high school…
