the angle is 41.81. yes the player can hack the turret.
The turret can be disabled, the angle is less the 45 degrees.
Theta = asin(4/6) = 41.81 degrees
My solution:
sin(𝚹) = 4/6
𝚹 = asin(4/6)
𝚹 = 41,81°
It is possible to hack the turret!
(I think…)
Solution :
Sin(Q) = Opp./Hyp.
= 4 / 6 = 2/3
Q = sin^-1(2/3)
= 41.81
Angle is less than 45 so the device should be able to disable the turret.
#spoiler
arcsine(4 / 6) = 41.81
Less than 45 degrees, so you can disable the turret.
We use sin(theta)=opp/hyp
So we have Sin(theta)=arcsin(4/6)=arcsin(0.66)=41.81
theta = asin(4/6)
theta = 41.81 degrees
It is possible to disable turret.
soh
A sin (4/6)=41.81
Hack is available
We’re looking at sin (or asin depending on how you want to do it) given we are concerned with opposite and adjacent edges and the angle.
The first way I did this was actually finding the opposite edge length for which the tech would be valid, so: sin(45deg)=opposite/6 => opposite = 41.81 app. which means that as long as the opposite side was less than 41 the tech would work.
Of course the other method is using arcsin(o/h)=41.81degrees which is smaller than 45 degrees maximum tilt.
Either way you arrive at the same answer - being that the tech will work.
it works at 41.81 degrees.
We have the opposite and hypotenuse lengths so we will use sine (sine = opposite/hypotenuse)
note: using Pythagorean theorem we could find the adjacent length and use tangent or cosine instead
is θ <= 45°?
sin(θ) = 4/6
θ = asin(4/6)
θ = 41.81°
Yes it is possible to disable the advice because θ is less than or equal to 45°
sin(a) = 4/6 = 2/3
a = 41,81
a < max Tilt
I am confused about sin cos and tan why do you use soh here? could anyone can explain here.
@garypettie @EddieRocks
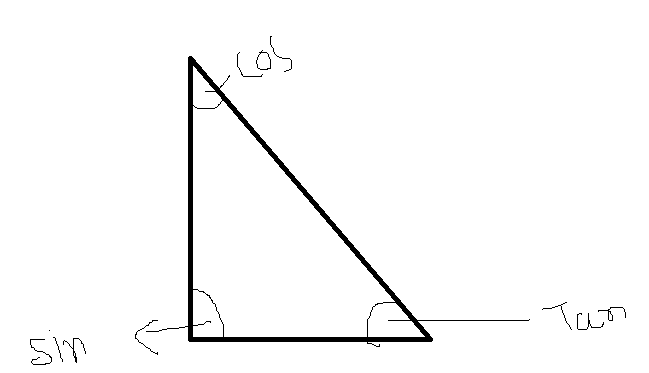
Great question @Rathod_Ketan!
It all comes down to what three pieces of information you know about your triangle.
For the challenge we know;
- That it’s a right-triangle
- the side opposite the unknown angle
- the hypotenuse of the triangle (the longest side).
Therefore, we need to use sin(θ) = opp/hyp.
If we quickly work out the missing side running (~4.472) then we can test the other options as well, as they should all give us the same angle:
θ = asin(4 / 6) = acos(4.472 / 6) = atan(4 / 4.472) = 41.81
The diagram you’ve drawn isn’t strictly accurate as sin/cos/tan are relational to the information you know about your triangle.
For instance, if we were looking for the angle by the turret then we’d use
θ = asin(4.472 / 6) = acos(4 / 6) = atan(4.472 / 4) = 48.19
I hope that helps clear things up for you.
thanks for answering sir I really appreciate it I get my answer but after completing section 3 in the math course I do not get enough knowledge to implement this logic in unity3d or 2d because there are only on paper examples we need unity examples. if you do not mind please check this video how that sir explain with real-time examples in unity
and
please update course examples with unity examples. because it’s hard to implement 
GameDevHQ is a great channel!
The reasons we don’t have specific coding examples is because we didn’t want to tie the course to a particular engine or programming language.
Unity, Unreal, Godot - They all have slightly different libraries and ways of coding things but the underlying math will always be the same. That’s why I try to focus on the underlying principles and point you in the general direction of common libraries that may help you along the way.
When coding up your own solutions, I’d strongly recommend starting with a base fomula as your pseudo-code and then start replacing the variables with actual code.
I hope that helps.
Thanks, sir for your response, but I improve my math and query search/solve skills also. this course helps me a lot more then I expect.
That’s great to hear 
sin(θ) = opposite / hypotenuse
sin(θ) = 4/6
θ = asin(4/6)
θ = 41.81°
θ is less than the max till, so the player can disable the turret.
This took me a little research. I still do not believe I fully grasp what function to use where. I know we went over sine, cosine, and tangent - but I feel like all of the instruction regarded finding lengths and sides. I wasn’t sure how to find angles! I did a little web browsing to figure out how to employ arc types, though. Hopefully this is correct!
Since we were trying to find Θ instead the sine, cosine, or tangent of Θ, I utilized asin (since the undefined side we were looking for was adjacent to the angle):
Θ = asin(4/6)
(Sorry, used a calculator because I have NO conceptual understanding on how to determine what the value of sin or asin are.
Θ ≈ 41.81



