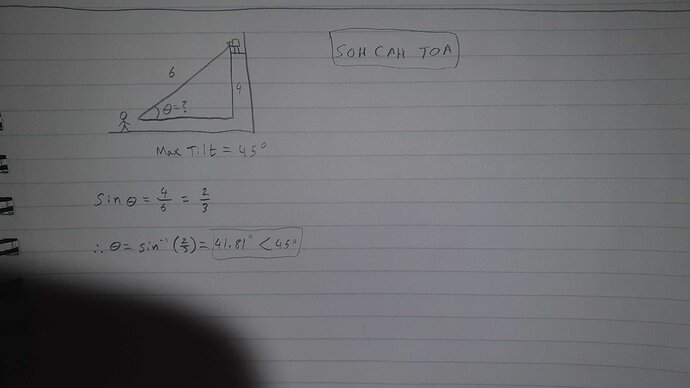Math - SOH CAH TOA - Challenge

Other Courses Talk
,
#1

In this lecture we looked at how to use SOH CAH TOA to find the missing angles in our right triangle and saw how we can also use the angle information to find the length of our sides.

What’s your favorite mnemonic for remembering SOH CAH TOA, or do you just remember it as is?

For your challenge, we want to know if our player can disable the turret given their rather poorly designed hacking device.

  • The turret is 4 units off the ground.
  • The hacking device has a maximum range of 6 units (the hypotenuse of our triangle)
  • The device stops working if tilted beyond 45 degrees.

Find the angle that the player has to point the device and give your answer to 2 decimal places.
Then confirm whether it’s possible to disable the turret (is that angle less than or greater than 45 degrees).

Post your answers below and remember to use spoiler tags.

#2

soh cah toa
s= o / h
sin(q) = 4/6
q = asin 4/6
q = 41.81
so can hack

3 Likes
#3

At first I was confused but then I realized you use asin or sin^-1. After I went back and used sin^-1 I got the same answer.

2 Likes
#4

@Kevin-Brandon, is there anything I can change to make things clearer?

It is both weird and annoying that there are two ways to write the inverse trig functions.
I’d argue that asin is a better way to write it. However, I do still tend to use the index notation version more because it’s the way I was taught and old habits are hard to break!

1 Like
#5

Hmm I think you explained it well. I just got confused in how I was supposed to get q. Then I realized I needed to use the inverse of sine. It’s more of the way I learn. I’m a hands on person so I didn’t fully understand it until I started working out the challenge.

#6

Most things in math take time and practice in order to stick, so keep it up the good work.

One key thing to remember is that you only need to use the inverse functions when you want to find a particular angle, since it’s the only way to separate it to get it on its own. For everything else, you can just leave them as they are.

1 Like
#7

Thank you Gary! Helping me get through geometry! I was horrible in high school. Mainly the proofs. Funny enough Trigonometry was my favorite math :thinking:

#8

Yeah, I hated writing proofs for stuff. I think it made me better in the long run though.

I mostly hated Trig at college, since I never saw the point of learning all the different identities for things like sec, csc, and cot, and I figured I’d never use all the hyperbolic stuff. Turns out I was wrong though and it turned out to be pretty useful thing to know after all!

My favorites were probability and combinatorics, so I’m looking forward to doing that section. :slight_smile:

#9

I get an angle of about 41.8° so yes we can hack the turret

1 Like
#10 
sin(a) = O / H
       = 4 / 6
       = 2/3

asin(2/3) = 41.81

So yes its possible to hack the turret.
2 Likes
#11

tan(theta) = 4/6 = 2/3

theta = atan(3/2)

= 56.31 deg / 0.98 rad

The player cannot disable the turret at the current distance.

But I’m confused about one thing - since we’re dealing with a right triangle here, wouldn’t the angle have to equal 45 degrees? Or am I missing something?

EDIT:
I goofed! the actual answer is atan(2/3) = 33.69 degrees. The calculator I’m using uses tan^-1 for arctan, so that mixed me up somehow.

#12

Hey @Ajai_Raj
For this problem the turret height is opposite the angle you’re measuring and the turret’s range is represented by the hypotenuse.
So instead of tan, you need to use the sin (tan = opp/adj and sin = opp/hyp)

For any triangle, the internal angles add to 180 degrees .
For a right triangle, where one of the angles has to be 90 degrees, the other two angles will sum to 180 - 90 = 90 degrees.
So whilst both angles being 45 degrees is a possibility, they don’t necessarily have to be.

1 Like
#13

Ohh I see. For some reason I was having a hard time visualizing a scalene right triangle, but I looked up some examples and it makes sense now.

So, using sin and arcsin, I got 41.81 degrees, meaning the player can disable the turret.

1 Like
#14

Spot on @Ajai_Raj!
A scalene triangle is one that has side lengths that are all different.
Whenever you deal with problems that involve right triangles you’ll most likely be dealing with the scalene version, since the isosceles version only exists when the internal angles are 90+45+45 degrees.

#15

sin=o/ℎ
sinθ=4/6=2/3
θ=asin⁡(2/3)
θ=41.81
41.81<45
So device will work on the turret

1 Like
#16

20200928_160522
20200928_1605224032×2268 235 KB

1 Like
#17

arcsin(theta) = 4/6
theta = 41,81°
It is possible to disable the turret as the angle is less than 45°.

1 Like
#18

sin(theta) = 4/6
asin(4/6) = theta = 41.81 degrees
41.81 degrees which is smaller than 45 degrees so yea, it would work, can hack.

1 Like
#19

Here is my answer:

kuva_2021-02-24_181910
kuva_2021-02-24_1819101226×343 10.1 KB

but I had problems doing this in an unreal engine. It seems to result in 0 always. Do you know what I do wrong?

Here is the code:
kuva_2021-02-24_182503
kuva_2021-02-24_194925

#20

Great work @Mikapo.
It looks like you’re trying to divide to integers, rather than two floats. If you do 4f / 6f then that should fix the problem.

Privacy & Terms