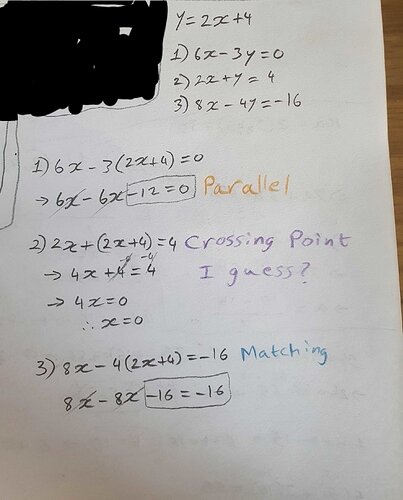In this lecture we learnt how to recognize when lines are parallel.
For your challenge, work out what the relationship is for each of these equations when comparing it to;
y = 2x + 4
One of them will be parallel, one will sit entirely on top of the original line, and one will cross it at some point.
Post your answers below and remember to use the spoiler tags.
6x - 3y = 0
They are parallel. Using substitution I found -4 = 0.
2x + y = 4
They cross at (0,4).
8x - 4y = -16
They are the same. Using substitution I found -16 = -16.
And to verify I transformed 8x - 4y = -16
(8x - 4y)/4 = -16/4
2x - y = -4
-y = -4 -2x
y = 2x + 4
Here are my solutions for these, after correction:
a) I get -12 = 0 by solving for y, so parallel
b) (0,4) intersection
c) 0=0 I guess that means they are the same?
I got these wrong so many times just out of silly mistakes like wrong signs, bad calculations and general rushing!
@olidadda, well done for persevering - It can be annoying to redo the same calculations over and over but it’s also great practice. 
For [c] you should have ended up with -16 = -16.
You can add 16 to both sides to get 0 = 0 but it’s not really necessary. if the numbers are the same on both sides then you know that the lines will sit on top of one another, so you can just stop there.
Thanks! Yeah I figured but writing 0=0 was like putting a nice big nail in the coffin of that equation.
Actually, the main thing was just to not rush and write things out neatly and everything became easy so lesson learnt!
haha, that’s one way to look at it!
Taking your time will definitely help avoid errors.
I’m actually guilty of making the same mistakes you mentioned when I’m rushing through things and not paying attention. I’m especially bad for it when coding and putting pluses where there should be minuses! 
I got:
@Ajai_Raj, you’ve got 1 and 3 right, but 2 is wrong.
Remember that you have to do the same thing to both sides, so;
2x + y = 4
isn’t the same as
y = 2x + 4
Give it another go and if you need some help, just let me know.
Oh, I see. Going back to it again, from adding the two equations together, I got 4 = 4. Graphing that, it means the lines intersect, correct?
@Ajai_Raj,
Here’s how to approach that second one:
You’re correct that the lines intersect but not for the reasons you give.
If you ended up with the equation being 4 = 4 then that would mean the lines are identical, but that shouldn’t have been the answer you ended up with.
Here are the 2 equations after rearranging and simplifying;
So they’re definitely not identical and the different signs in front of the ‘x’ mean they have opposite gradients.
Once you’re comfortable reading equations like these, you could probably look at them and also say that they intersect at (0,4) but if you wanted to work it out properly you could use one of the simultaneous solving methods.
Here’s the answer using substitution:
Substitute equation 1 into 2.
2x + (2x + 4) = 4
2x + 2x = 4 - 4
4x = 0
x = 0
Then solve for y;
(2*0) + y = 4
y = 4
I hope that helps.
Oh, the fond memories of math class. 
y = 2x + 4
6x - 3y = 0
6x - 3(2x + 4) = 4
6x - 6x + 12 = 4 => Parallel lines (no solution)
2x + y = 4
2x + (2x + 4) = 4
4x + 4 = 4 => x = 0
y = 2x + 4
y = 2*0 + 4 => y = 4
8x - 4y = -16
2x - y = -4
2x + 4 = y => Overlapping lines (same as first equation)
@KhaledAhmedYounes, you got all three correct.
For the second one, you’ve found that x = 0.
To find the exact point where the two lines cross just plug that answer back into the original equation and solve for y.
(2 * 0) + y = 4
y = 4
Therefore, the two lines cross at (0, 4)
Work below
8x−4(2x+4)=−16
8x−8x−16=−16
−16=−16
identical
2x+y=4
2x+2x+4=4
4x+4=4
4x=0
x=0
y=2(0)+4
y=4
6x−3(2x+4)=0
6x−6x−12=0
−12=0
parallel
1>parallel
2>intersect
3>sit over it
i still remember this all cuz i am still in class 12th and this all is appearing to me repeating
(Identical Lines, Green and Orange)
CHALLENGE!
y = 2x + 4
What is the relationship to this particular one??
One of these will be parallel, one will sit on top, and one will have a single crossing point
6x – 3y = 0
+3y +3y
3y = 6x
/3 /3
y = 2x
This line is parrel to the example line
2x + y = 4
-2x -2x
y = -2x + 4
This line intersects with the example line
8x – 4y = -16
+4y +4y
4y – 16 = 8x
/4 /4 /4
y – 4 = 2x
+4 +4
y = 2x + 4
This line sits directly on top of the example line.
1) it is parallel
2) this one intersects
3) this one sits on top.
I used substitution for this challenge
So for the first one I got -12 = 0. So the lines are parallel
For the secone one I got x = 0 y = 4 so the lines are crossing
And for the third one I got -16 = -16 So the line sit entirely on top of the original line
