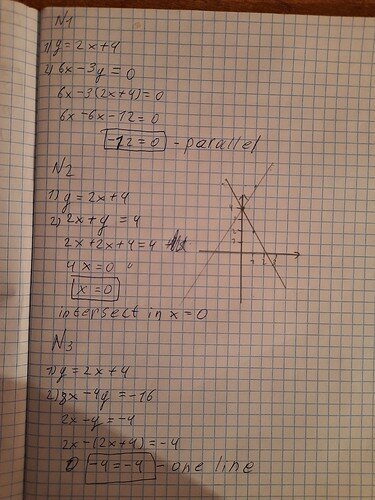My results are:
︎ parallel︎ single point intersect︎ on topEquation
6x - 3(2x + 4) = 0
6x - 6x -12 = 0
-12 = 0
Equation
2x + 2x + 4 = 4
4x + 4 = 4
x + 1 = 1
x = 0
(I drew this one out. I am not sure the equation makes sense in this case. I can’t see how this result connects to the graph.)
Equation
8x - 4(2x + 4) = -16
8x - 8x -16 = -16
-16 = -16
Great work.
For the second one, you don’t really have to solve anything, unless you want to find the point of intersection. You could just get away with rearranging things to prove that they intersect at some point.
The reference equation is y = 2x + 4, and if we rearrange the second one we get:
2x + y = 4
y = -2x + 4
From this, we can see that the gradients are different, so they must intersect at some point.
Taking what you’ve got for your answer, you’ve proved that there is a single valid answer for x, which also shows that they intersect.
In fact, you’ve found the x-value for the point of intersection, so you could always substitute that answer into one of the equations to find the y-value as well. In this case, the intersection occurs at the point (0, 4).
Ha, yes indeed. Now I also see the intersection point of y = 4 in the original formula and it adds up with the x = 0! That was my drawing result too. Geez, math is fun. 
So here is my answer:
1
y = 2x + 4
6x - 3y = 0
6x - 3(2x + 4) = 0
6x - 6x - 12 = 0
-12 = 0
Answer: Because the result is false these two lines are parallel lines
2
y = 2x + 4
2x + y = 4
2x + 2x + 4 = 4
4x = 0
x = 0
They will intersect each other when x = 0 so I will solve y now
y = 2 * 0 + 4
y = 4
Respond: These lines will intersect when x = 0 and y = 4
3
y = 2x + 4
8x - 4y = -16
8x - 4(2x + 4) = -16
8x - 8x - 16 = -16
0 = - 16 + 16
0 = 0
Respond: Because the result is true always it means that lines are top of each other
2x+4
6x-3y = 0 is parallel, it can be rearranged as y = 2x, having the same slope.
2x+y = 4 has a opposite slope, and the equations intersect at (0,4)
8x-4y = -16 can be rearranged into the same equation, meaning it will sit entirely on top of the original line.
This is what I got :
y = 2x + 4 == 8x -4y = -16 lines on top of each other , gradient 2
6x - 3y = 0 runs paralel to y 2x + 4 through (0,0) gradient 2
2x +y = 4 intersects the above lines. y = 2x +4 (both of them) and 6x - 3y =0
at (0,4) and (1,2). which I determined through substitution.
I graphed it out to confirm. Hope I didn’t miss anything.
1: Parallel
2. X=0, Y = 4,
3. Same
Starting line: y = 2x + 4
Rearranged equation: y = 2x.
Which line would be parallel with the starting line.
Rearranged equation: y = -2x + 4.
This line is crossing the starting line.
Rearranged equation: y = 2x + 4.
This would mean that the line is on top of the starting line.
The first cross the equation at the point (0,4)
The second is parallel
The third is the same equation(so it sits on top of the original line)
Good morning,
Here is my response:
1- Parallel
2- Intercept only on ( y ) as x = 0
3- They are the same
Cheers!
my response is 1 is y=2x which is parallel
2 is y=-2x +4 which is perpendicular
and 3 is another y=2x+4 which is the same line just in another format.
1) Parallel
2)Intersecting (specifically at x=0; y = 4)
3)Equivalent
I simplified each first, then decided the answer based on the data, and then graphed the equations to check my decisions.
6x - 3y = 0
6x - 3(2x + 4) = 0
6x - 6x - 12 = 0
-12 = 0
-12 are not equal to 0, so they are parallel.
2x + y = 4
2x + 2x + 4 = 4
4x + 4 = 4
4x = 4 - 4
x = 0
y = 2x + 4
y = 0 + 4
y = 4
The two lines cross at (0, 4)
8x - 4y = -16
8x - 4(2x +4) = -16
8x - 8x -16 = -16
-16 = -16
Lines are identical
Hah! This took some going back and doing some major review. (Particularly for #2)
1.) (-12) = 0 – Runs Parallel
2.) Intersects at (0, 4)
3.) (-16) = (-16) – Sits On Top
Here’s my answers for the Parallel Lines challenge:
Q1. 6x - 3y = 0
A1. Parallel
Q2. 2x + y = 4
A2. Single intercept
Q3. 8x - 4y = -16
A3. Same equation
