In this lecture we looked a simple way of factoring our equations, without having having to learn the rather cumbersome quadratic formula. This method helps us to convert our equation from standard form into intercept form and also tells up how many roots our equation will have.
For your challenge, convert the following equation into intercept, or factored, form;
y = -1/3x^2 + 10/3x - 16/3
Post your answer below and remember to use spoiler tags.
y = -1/3x² + 10/3x - 16/3
-3y = x² - 10x + 16
10/2 = 5
so (5 + u)(5 - u) = 16
25 - u² = 16
u² = 25 - 16
u = √9
u = 3
5+3 = 8 and 5-3 = 2
so y = -1/3 (x - 2)(x-8)
we can see that (2,0) and (8,0) are our roots like before.
y = -1/3 (x-2)(x-8) Roots: (2,0) and (8,0)
-3y = x^2 - 10x + 16
(5+u)(5-u) = 16
25 - u^2 = 16
-u^2 = -9
u = 3
(5-3)(5+3) = 2 x 8 = 16
y = -1/3(x-2)(x-8)
Yeah!! 
y = -1/3x^2 + 10/3x - 16/3
Convert to intercept form.
-3y = x^2 - 10x + 16
(-5-u)(-5+u)=16
25-u^2=16
u^2=3
-3y = (x-8)(x-2)
y = -1/3(x-8)(x-2)
y=−(1/3) x^2+(10/3)x −(16/3) −Convert to intercept form
−3y=x^2−10x+16
(5+u)(5−u)=16
25−u^2=16
−u^2=−9
u=3
(5+3)∗(5−3)=16
(8)∗(2)=16
y=−(1/3)(x−8)(x−2)
My results are:
y = -1/3x² + 10/3 - 16/3
-3y = x² - 10 + 16
(5 - u)(5 + u) = 16
25 - u² = 16
u² = 25 - 16
u = √9
u = 3
(5 - 3)(5 + 3) = 16
(2)(8) = 16
(2,0) (8,0)
I was able to follow this along using your method. But what I am not getting really is how we get from
(5 - u)(5 + u) to 25 - u²
and from
25 - u² = 16 to u² = 25 - 16!
It’s probably fairly simple but I am somehow missing it. If you have a minute could you explain that please?
Hi @TheSnooze,
We can get from (5 + u)(5 - u) to 25 - u^2 by expanding the parentheses.
For this, you can use the FOIL method.
Then it’s just a case of rearranging the equation.
Here are the full steps,
(5 + u)(5 - u) = 16 <- expand parentheses using FOIL
25 - 5u + 5u - u^2 = 16 <- -5u + 5u cancel out
-25 + u^2 = -16 <- multiply both sides by -1
u^2 = -16 + 25 <- add 25 from both sides
u = √9 <- take the square root of both sides
u = 3 <- simplify
Once you get used to manipulating equations, you’ll find that there are a few shortcuts that you can take to speed things up - Such as expanding binomials in the form (a + b)(a - b) = a^2 + b^2 or learning combining the step of multiply by -1 with another action, like moving things from left to right.
I hope that helps.
Dang. I tried to use the FOIL method but somehow it wasn’t adding up. Guess my math brain needs some more working on… Thanks for your time. It makes total sense now!
And on the second problem the multiplying by -1 is what I missed. (But shouldn’t it be “-25 + u^2 = -16” after multiplying by -1?)
Yes it should - good spot! That was a typo on my part and proof that it happens to all of us! 
(I’ve now edited the original response).
Right on… My math brain starts engaging.
For y = -1/3x^2 + 10/3x - 16/3:
-3y = x^2-10x+16
(5+u) (5-u) = 16
u^2 = 25 - 16
u^2 = 9
u = 3
y = -1/3 (x-8) (x-2)
the answer is y=(-1/3)x^2+(10/3)-(16/3)=(-1/3)(x-8)(x-2)
y = -1/3(x - 2)(x - 8)
Tried this way first because I was struggling with the method explained
y = -1/3x^ + 10/3x - 16/3
-3y = x^2 - 10x + 16
y = 0 because we are working on the intercept
0 = x^2 -10x +16
complete the square 0 = (x +(-5) )^2 - (-5^2) + 16
9 = (x - 5 )^2
3 = x - 5 or -3 = x - 5
x = 8 or x = 2
intercepts are (2,0) and (8,0)
After a lot of reviewing the lesson I managed this
d
-3y = x^2 - 10x + 16
if I understand correctly then (1/2 b + u ) (1/2b - u) = c
I have to flip the sign of b here ( nut sure why yet)
so (5 + u)(5-u) = 16
25 + 5u - 5u - u^2 = 16
-u^2 = 16 - 25
u^2 = 9
u = 3
5 + 3 = 8
5 -3 =2
intercepts are (2,0) and (8,0)
and I’m lost again
The first way came to me intuitively but I really had to work at the second one.
Which way is preferable to use ( is the first method even correct) ?
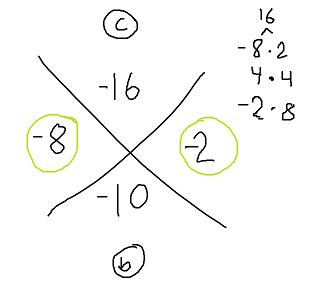
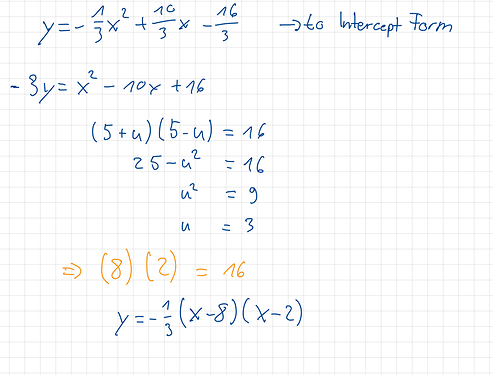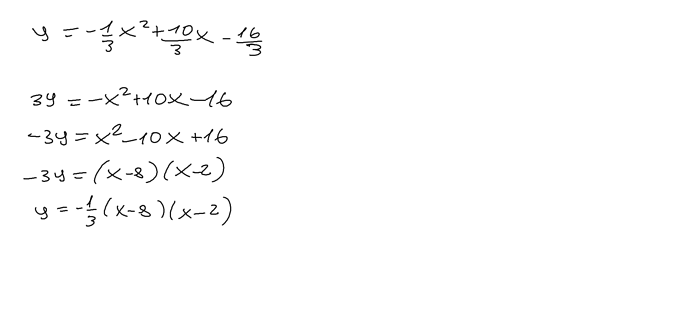Hi @Manie_Besselaar,
You can definitely solve quadratics using the first method of “completing the square” but it can get a little tricky depending on the coefficients you’re working with.
In the worst case, you end up having to fall back on the good old quadratic formula - i.e. y = (-b ± √(b² - 4ac)) / (2a), which can be a pain to try and memorize and usually requires a fair bit of work to simplify at the end.
I find that the method I showed in the video is a bit more intuitive because the process is always the same.
It can also give you an earlier warning on whether you’re dealing with a parabola with real or imaginary roots, which can be nice.
There’s not really a universally “preferred” way to solve any equation and there are always different ways to approach any problem. For instance, this method was only popularized in 2019 by the mathematician Po-Shen Loh!
If you’d like some additional insight into the method then I’d recommend checking out Loh’s excellent explanation here: https://www.poshenloh.com/quadraticdetail/
(His video explanation is about ~40mins long so grab a drink and settle in!)
Thank you.
After getting my head around the method you demonstrated in the video it was definitely easier. I also found myself getting a little stuck when trying to complete the square on the equations where there was no intercept.
Then again this is the first time since 1996 that I have seriously sat down to do math, so I most probably need a lot of practice.
I struggled a bit with this video. I went back to the traditional method of solving this (Sorry!).
Edit: @garypettie I just saw that you linked Po-Shen Loh’s explanation of this method. I will definitely watch that too. Hopefully it will result in an epiphany
Standard form:
y = -1/3x^2 + 10/3x - 16/3
Factor out the fractions by dividing by (-1/3):
y = -1/3(x^2 - 10x - 16)
Using the AC method to check what number to multiply with to get to -16, and add to get to -10:
Answer:
-1/3(x - 8) (x - 2)
