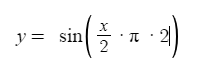Hi Ihshan,
What is the purpose of this line if (period <= Mathf.Epsilon) { return; } . It says that to protect against period is zero. Could you explain to me that comment please ?
Log Mathf.Epsilon into your console. You’ll notice that it is a value which is almost 0. Actually, you could have written period == 0 because Mathf.Epsilon is usually used when calculating with floats. All number types in programming are unprecise meaning you do not have a definite number of digits behind the dot. It might be that you are calculating something which is actually 0 but due to the unprecise type, the result is not 0 but 0.000000001 or something like that. It’s an example to visualise the problem.
To solve this, programmers invented Mathf.Epsilon which generates a very low value which is almost 0 to compare a result with it and treat it as though it was 0.
Why do we need this code at the first place ? do we we want to make the movement of an object (in this case Obstacle) smoother ?
Not smoother but it is supposed to appear more interesting. It’s difficult to explain. Go to this website and test the different curves to see how the function affects the movement. Ben is doing something similar with the sine function. You can imitate a part of the sine curve on that website and compare it to the linear movement.
What does the comment mean “//grows continually from 0`” ?
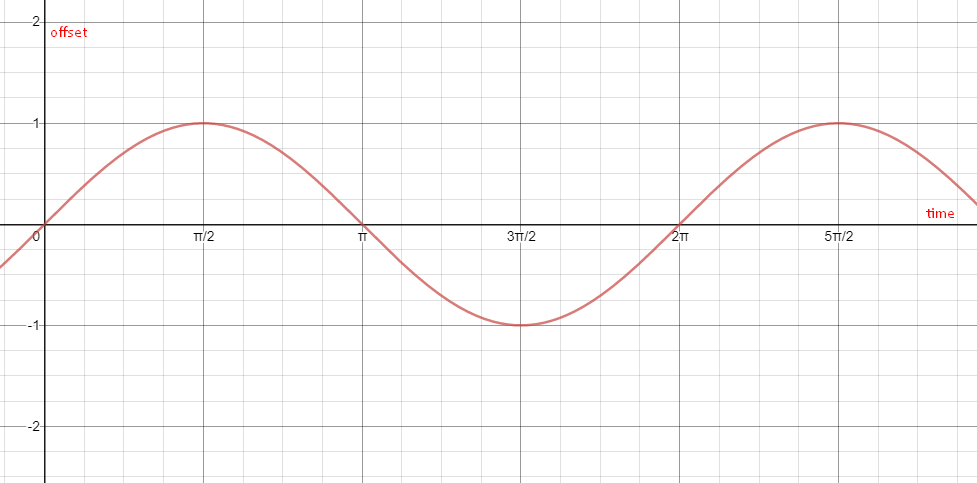
The time starts at 0. 0 seconds, 0.12 seconds, 0.245 seconds, and so on. 1001.02 seconds. You have two axes: time and offset in your imaginary diagram. The offset ranges from -1 to 1, and the time starts at 0 and never ends. With your function, you could pass on 1001.02 seconds to get the offset at this particular moment.
Maybe it helps if we take a brief look at a sine wave. I really like this website:
https://www.desmos.com/calculator/w9jrdpvsmk
I labeled the horizontal axis “time”, and the vertical axis “offset”. When you execute float offset = Mathf.Sin(Mathf.PI / 2);, you get offset == 1. Can you tell me what the result of Mathf.Sin(3f * Mathf.PI / 2) is just by looking at the curve and the axes? If you can do that, you know how Ben utilises this curve.
Pi is approximately 3.14. If we define the horizontal axis in time in seconds, this would mean that the offset is 0 at 3.14 seconds. Time.time represents the game time in seconds.
Does that make sense so far?
If so, we can get this curve by passing on Time.time to the sine method:
float rawSineWave = Mathf.Sin(Time.time);
However, 3.14 is a fairly inconvenient value to intepret. How fast does our object move back and forth completely? According to our wave (see above), it’s 2*PI seconds, 6.28 seconds. Wouldn’t it be nicer if we could say it takes 1 seconds?
float tau = Mathf.PI * 2f;
float rawSineWave = Mathf.Sin(Time.time * tau);
I changed the step to 1 on the x-axis, and I get this result:
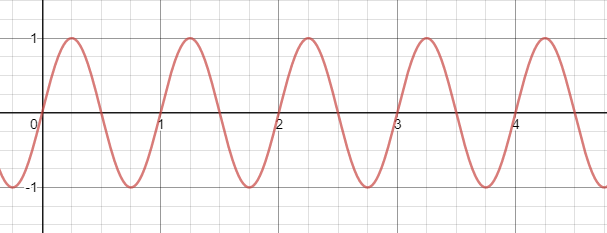
Now, what happens if we manipulate Time.time by dividing it?
float cycles = Time.time / 2f;
float tau = Mathf.PI * 2f;
float rawSineWave = Mathf.Sin(cycles * tau);
Type the values yourself on the linked website and toy around with them.
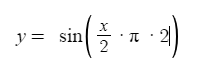
As you can see, the remaining problem is that the values on the y-axis range from -1 to +1. We want 0 to 1.