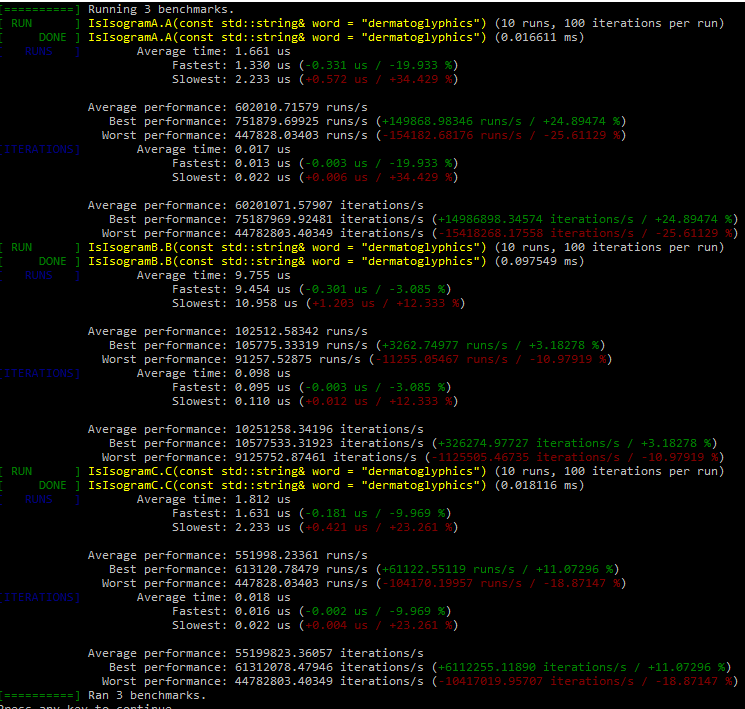
There were two algorithms proposed for determining if a word is an isogram or not:
Method A – The kind of brute-force method, which compares each letter to every other letter. The actual order for this one is ((n^2) - n) / 2.
Method B – A more clever method in design, this approach first sorts the word (which has its own cost that we will include) and then it loops through the sorted word and checks each contiguous pair for a match. The actual order for this one is (n log n) + (n - 1).
First it’s important to keep in mind what the order expression is really describing. It’s describing the MAXIMUM number of comparisons that an algorithm can possibly make when determining if the word is an isogram. Obviously, a well-designed algorithm should return the answer as soon as it has it. The maximum number of comparisons WILL be made if in fact the word is an isogram, otherwise the good algorithm will be able to make less comparisons before determining that the word is not an isogram.
So to see how the two methods compare when the word is in fact an isogram, we plot it on the graph using:
(((n^2)-n)/2) vs ((n log n) + (n - 1)), n=2 to 15
Copy/paste that into the http://www.wolframalpha.com site.
I went to 15 because the largest isogram known is “dermatoglyphics”. But you should also run the range at 26 and beyond to really see how method B really scales well at longer string lengths, even though 26 is the highest valid value.
If you look closely, you’ll see that it’s only at 7 characters and beyond that method B begins to be more efficient. Shorter than that, method A utilizes less comparisons. Don’t forget, we are including the comparisons that are required to run the sort() method.
And again, we are comparing the efficiency of the two methods only when the word is an isogram and therefore will “stress” the algorithms to the max. If the word is not an isogram, then which method is faster will depend on a couple factors: how long is the word and which character is repeated?
If the word is long, then sorting it will have a high cost, possibly making method A faster. If the letter that’s repeated comes soon in the alphabet (like the letter “a”), then method B may end up being faster (because the word is sorted first and then searched for pairs). If the letter that is repeated comes soon in the word itself, then method A will be faster. If there is a letter that is repeated often (more than twice), then method A will be faster as well.
So what’s my vote? If I had to vote, I would say in a practical sense method A is faster. That’s because most common isograms will be less than 7 letters, many commonly used words are less than 7 letters, and many words are not isograms, with the repeating letters coming soon in the word. 
Remember that a well-designed algorithm will return the answer as soon as it has it!
Here’s the code to prove all this. Just change the first line in main() to test whatever word you want.
#include <stdio.h>
#include <tchar.h>
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <math.h>
using namespace std;
void IsIsogramA(const char* word, int size)
{
bool isIsogram = true;
int count = 0;
for (int i = 0; i < size; i++)
{
char currChar = word[i];
for (int j = 0; j < i; j++)
{
char compChar = word[j];
count++;
if (currChar == compChar)
{
cout << count << " comparisons made with Method A and NO, it is not an isogram." << endl << endl;
isIsogram = false;
break;
}
}
if (!isIsogram) break;
}
if (isIsogram)
cout << count << " comparisons made with Method A and YES, it is an isogram." << endl << endl;
}
void IsIsogramB(const char* word, int size)
{
string strWord(word, size);
sort(strWord.begin(), strWord.end());
bool isIsogram = true;
int count = (int)(size * log(size));
for (int i = 0; i < (int)strWord.length(); i++)
{
if (i >= (int)strWord.length() - 1)
{
break;
}
else
{
count++;
if (strWord[i] == strWord[i + 1])
{
cout << count << " comparisons made with Method B and NO, it is not an isogram." << endl << endl;
isIsogram = false;
break;
}
}
}
if (isIsogram)
cout << count << " comparisons made with Method B and YES, it is an isogram." << endl << endl;
}
int main()
{
string word("dermatoglyphics");
cout << "Is \"" << word << "\" an isogram? " << endl << endl;
IsIsogramA(word.c_str(), word.length());
IsIsogramB(word.c_str(), word.length());
cin.get();
return 0;
}
