when the Log of 1000 = 3 I can prove it by multiplying it out…
10 x 10 x 10 = 1000
However, as in the video’s example: the Log of 3000 = 3.47712. How do I multiply that out to prove it?
** P.S. I’m not looking for the answer of 10 ^ 3.47712
1 Like
Hi @Kyle_Manning, the math required to do this by hand is pretty involved and is outside the scope of this course, but I’m happy to give you a brief explanation of how to approximate an answer using the Taylor series (which you could theoretically do by hand).
My honest recommendation though is to just use a calculator, since it’s far quicker and simpler!
So for this particular problem, it’s perfectly fine to say that Log(3000) ≈ 3.47712 so 10^(3.47712) ≈ 3000.
But let’s look at how to get there using the Taylor series for e^x and no calculator at all (you’ll be doing a lot of long multiplication and division);
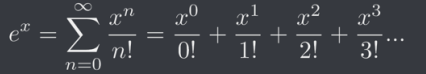
That equation is a lot to take in at this stage of the course, so you don’t really need to worry about the sigma notation part. I’ve broken out the first few terms, so just continue following that same pattern until you converge on an answer that’s close enough.
And since this is working with e^x we need to find the natural log of 3000 instead.
So ln(3000) ≈ 8.00637.
If you’ve not encountered the factorials before, Ben covers these in few lectures time.
They’re pretty straight forward though, you just take the number and multiply it by every whole number that came before it.
For example,
1! = 1,
2! = 2 * 1,
3! = 3 * 2 * 1
and so on.
Now it’s just a case of going through the infinite sum until you converge on an answer to the level or accuracy that you need.
This can take a while, but with every new term that you add you’ll get a bit closer to the final approximation.
So if we say x = 8.00637 these would be the total sums as we add new terms to our series.
(written below as [#terms] : [answer])
1 : 1
2 : 9
3 : 41.1
4 : 126.6
5 : 297.8
6 : 572.0
7 : 937.8
8 : 1356.2
9 : 1775.0
10 : 2147.5
11 : 2445.8
12 : 2662.9
13 : 2807.7
14 : 2896.9
15 : 2947.9
16 : 2975.1
17 : 2988.8
18 : 2995.2
19 : 2998.0
20 : 2999.2
21 : 2999.7
22 : 2999.9
23 : 3000
So we need to work out the first 23 terms before we finally converge on the answer of 3000.
It’s definitely a long and tedious job to do it by hand and, since it’s only an approximation, you’ll never get an exact result. So you need to account for that and choose your level of precision wisely.
For example,
If you rounded ln(3000) to 8 then you’d converge on 2981 rather than 3000.
If you used 8.006 your converge on 2998.9
Anyway, I hope that helps explain how you might check your calculation by hand and also highlights why you probably don’t want to!
4 Likes
Thanks Gary,
The answer is as complex as I was suspecting. I just wanted to make sure that it wasn’t something simple that I was overlooking.
phew ~~ I feel better.
2 Likes
Yep, doing it by hand is not for the feint of heart! It’s not overly difficult, just very very long winded.
That’s why, before the invention of calculators, people would use slide rules and log tables to quickly get to an answer.
It is slightly easier if you have a rational exponent, since you can use the index laws to help rearrange things. But even then you’ll be left with something that can take a while to convert into a decimal number at the end.
Anyway, I’m glad I could help.
If you couldn’t quite follow it all at this stage, come back at the end of the course and it should make a lot more sense.
4 Likes
Thanks for the detailed explanation. I understand the sigma and factorials. But what is the value of x at each iteration?