One root and one point

[Yee]

@garypettie

Is there any way to calculate a parabola with the following info:

• One root = (1, 0)
• A point where the parabola should pass = (4, 3)
• The Y value of the vertex point = (x, 5)
  – x > 1 & 4 > x

I’ve tried multiple methods, but can’t seem to make it work . Any ideas?

I didn’t know the topic would close after being marked as solved…
Thanks for the amazing solution! It was driving crazy.

[garypettie]

Hey @Yee, apologies for the delay in responding. I don’t frequent the forum as much as I’d like (or probably should!).

This problem is totally possible but can be a little long-winded, so buckle up!

First, let’s look at what we know:

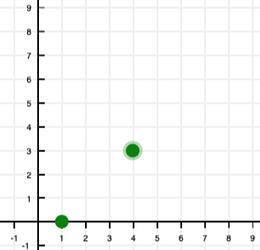
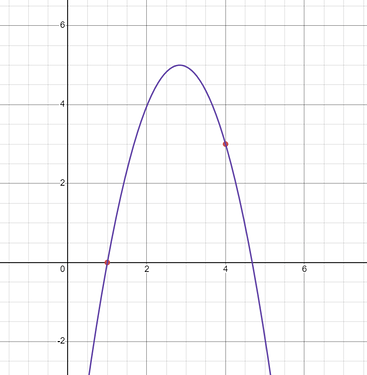
1. The parabola passes through points (1,0) and (4,3)
2. The height of the vertex is 5
3. The x-coordinate for the vertex should be between 1 and 4

This should be enough information to solve the problem but it’s going to take pretty much every trick in the book to get there. Note that point 3 is very important in making sure there is only one solution here.

For reference, this is the line we’re trying to find:

Before we dive down the rabbit hole, let me walk you through the general process:

1. Start by plugging in what we know into the vertex form - this is pretty much just the height at this point.
2. Make yourself two versions of this equation using the two known points (1, 0) and (4, 3).
3. Isolate the a term in the first of these equations and then use substitution on the second one to get a quadratic with only one unknown term - h.
4. Use the quadratic formula to find the value for h.
5. Plug that value back into your vertex form equation for point (1, 0) to find the value of a.
6. You now have concrete values for a, h, and k, so you can now solve your equation!

As you can see, it’s a pretty involved process, so grab your beverage of choice and let’s dive in!

---

Step 1

Let’s start with the vertex form for our quadratic equation.

(i)
y = a(x - h)² + k

h and k are the vertex coordinates, but we only know the height. That’s fine, one term down, two to go!

(ii)
y = a(x - h)² + 5

---

Step 2

With that, let’s look at finding some useable equations using our two known points.

For point (1,0), we get:

(iii)
y = a(x - h)² + 5
0 = a(1 - h)² + 5
-5 = a(1 - h)²

For point (4,3), we get:

(iv)
y = a(x - h)² + 5
3 = a(4 - h)² + 5
-2 = a(4 - h)²

---

Step 3

We can now solve a simultaneous equation by substitution to get down to only one missing variable.

First, let’s isolate a in equation (iii):

(v)
-5 = a(1 - h)² + 5
a = -5 / (1 - h)²

Now sub that into equation (iv):

(vi)
-2 = (-5 / (1 - h)²) * (4 - h)²
-2(1 - h)² = -5(4 - h)²
-2 + 4h - 2h² = 90 + 40h - 5²
0 = 3h² - 36h + 78

---

Step 4

Right, now we’re cooking! We have a quadratic formula with a single variable, so let’s solve for h:

a = 3
b = -36
c = 78

(vii)
h = (-b ± √(b² - 4ac) ) / 2a
h = (36 ± √(-36² - (4 * 3 * 78)) ) / (2 * 3)
h = (36 ± √360) / 6
h = 6 ± √10

Now, we can discard one of these, as we have the constraint that our value should be somewhere between 1 and 4, so that leaves us with:

h = 6 - √10

---

Step 5

Still with me?
Good.
We’re almost there…

Let’s actually go back to our vertex form for the point (1, 0) and find a concrete value for a.

(viii)
0 = a(1 - h)² + 5
0 = a(1 -  (6 - √10))² + 5
-5 = a(35 - 10√10)
a = -(7 + 2√10) / 9

---

Solution

Huzzah, if you made it this far I tip my cap you you! We basically have our answer.

y = a(x - h)² + k
y = (-(7 + 2√10) / 9) (x - (6 - √10))² + 5

To make this easier to read, here’s a properly formatted image:

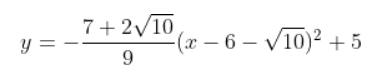
If you just need a decimal approximation for this, you could get away with:

y = -1.4805 (x - 2.8377)² + 5

I’m not going to lie, this did take me a while to crunch though and type up. It was a fun little challenge though!
All the tools used to arrive at the solution are covered in the course, so there shouldn’t be any major surprises.
If you’d like any additional explanations for any of the steps though, let me know (Hopefully I didn’t make any mistakes in there!).

Also note that this likely isn’t the only way to do it - just the way I reasoned through it