Shouldn’t 50 metres per second be 50 x ms^-1 ? In other words 50m/s?
Ben explains this in the video but it’s really not very clear what he means.
Hi @olidadda, you don’t need to add in a multiplication sign between the value and the units.
50 ms^-1 is exactly the same as 50 m/s, it’s just a different way of notating it.
To explain why, I need to explain one of the basics of index notation (you may also hear it called exponent or exponential notation).
For reference I covered the various index laws in this post: How the X value was fully obtained? and we introduce them at various points in the course when they become relevant.
At this point in the course we’ve already looked at things like square numbers (x^2) and cube numbers (x^3) but we can also make these exponents negative.
And when we do that, you’re representing a fraction.
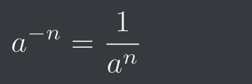
So if we imagine this with numbers, we could say that;
1/2 = 2^(-1)
and you can run that through your calculator to confirm that is the case.
Now if we replace these numbers with our units, the same rules apply, so;
m/s
= m * 1/s
= m * s^(-1)
= ms^(-1)
Even though this notation can be a little hard to read when you first encounter it, it’s worth learning as it makes life a lot easier in the long run.
As an example let’s say you were measuring acceleration, which is in meters per second squared, or meters per second per second.
you could write this as;
m / (s*s)
m / s / s
m / (s^2)
or
ms^(-2)
I don’t know about you but I much prefer that last option.
And if you start adding in more than two units, like Ben’s example of meters per second per dog (… ummm… ok) then you can write this concisely as;
ms^(-1)d^(-1)
which is better than the alternative of something like;
m / s / d
m/s * 1/d
etc.
Anyway, I hope that helps clarify things for you. If you have any other questions, just ask. 
2 Likes
Hi there, yes that’s all clear, but it doesn’t really address the point I was raising:
In the video, Ben marks the y axis with numbers such as 50, and then he writes 50 DIVIDED by ms^-1
If ms^1 is the unit of measurement and the 50 is how many of these we have, then why are we dividing by it? If anything there is an implicit multiplication as in 50 * ms^-1 = 50ms^-1
On a side note, from your explanation I gather also that if we have a fraction of a fraction, like a/b/c, we should be able to interchange the two denominators, in this case b and c without the value changing because that’s equivalent to a * b^-1 * c^-1 = a * 1/b * 1/c = a/b/c = a/c/b and as far as I know, we can perform multiplications in any order, is that right?
Ah, you’re talking about the axis labels correct?
Personally, I’m not a fan of notating my axes in that way but it’s a preference thing.
The slash there is just being used as a separator between the name and the unit of measurement. So it’s not representing a division.
Instead of using a slash I tend to wrap my units in parentheses, so instead of;
“speed / ms^(-1)”
I use
“speed (ms^(-1))”
Neither is inherently correct or incorrect. It really is just a preference thing.
In answer to your other question… it depends on the context and you really want to avoid stacking fractions where possible.
For example do you mean;
a ÷ b ÷ c
(a ÷ b) / c
or
a ÷ (b ÷ c)
Let’s say a=2, b=4, c=8
(2 ÷ 4) ÷ 8 = 1/16
(2 ÷ 8) ÷ 4 = 1/16
2 ÷ (4 ÷ 8) = 4
2 ÷ (8 ÷ 4) = 1
So how you separate things matters and it’s easy to make a mistake and misinterpret what’s been written - It’s how most of those viral math problems try and get you.
It’s also why index notation is useful. It removes any ambiguity since you can multiply in any order you like.
2 * 4^(-1) * 8^(-1) = 1/16
regardless of which order you put them in.
1 Like
Thank you Gary,
I’m glad that resolves the issue of axis labels, I too will opt for the brakets as it seems more intuitive.
Cheers,
Oliver
Always happy to help.
1 Like
This topic was automatically closed 24 hours after the last reply. New replies are no longer allowed.