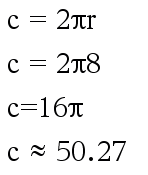In this lecture we introduced the circle constant π (Pi) and found out where this number comes from.
We also looked at its lesser known cousin τ (Tau).
For your challenge, find the circumference of a circle which has a radius of 8 units.
You can give your answer in terms of π, τ, or to 2 d.p.
Post your answer below and remember to use the spoiler tags.
52.27
16π
8τ
My answer is different to the Eddie’s above… not sure if I made a mistake?
I get 2pi*(8) = 50.26
Good spot.
@EddieRocks, your decimal representation is off. You got the right answers in terms of pi and tau though.
@olidadda, your answer is slightly off due to a rounding error.
The correct answers should be;
16π = 8τ = 50.27 (2 d.p.)
Oops… I really need to learn to read and type correctly…
Me too! 
In the lecture we learned C / D = PI which means C = PI * D
Now the diameter equals to 2 * radius.
–> C = PI * 2 * R
Using the numbers of the example
=> C = PI * 2 * 8 ^= 50.27
r = 8
c = 2 * pi * 8
c = 16(pi)
c = ~50.24
Nice work @ajai.
Just be careful when using rounded values to make sure you don’t introduce rounding errors.
if you do round early then it’s usually a good idea to keep 1 or 2 extra digits beyond what you’re final answer will use.
So rather than using 3.14 for pi, try using 3.142 or 3.1416, which would give you an answer that rounds to 50.27.
50.27
Given r = 8
Find the circumference
c = 2πr
c = 16π
c = 16 Pi
C = τr
c = τ(8)
c = 2π(8)
c = 50.27
c = 2πr
c = 2π8
c = 50.27
Here’s my result:
C/16 = 𝛑
C = 16𝛑
C = 50,27
here is mine:
C = 16 Pi, or 50.27
C=16pi or 50.27
tau- that is 6.18, I used only first two decimal digits - * 8 = 50,26
Great work @Gianni.
As a general rule of thumb, it’s a good idea to avoid premature rounding because errors can quickly start to stack up.
If you do decide to round early, always try to keep an extra couple of digits of precision during your calculation, so that you still have room to do a final rounding step at the end. In this case, that would mean using τ to around 4 d.p.