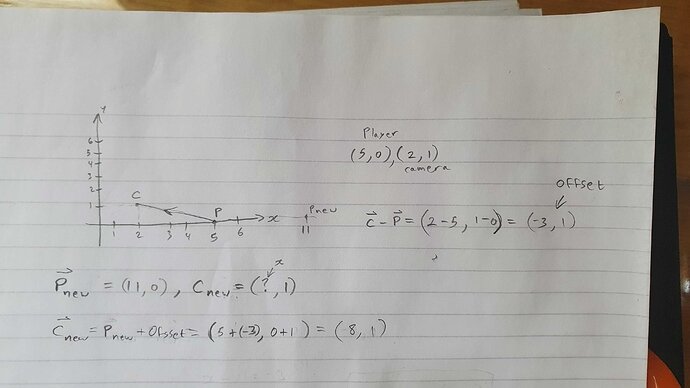Math - Vector Addition - Challenge

Other Courses Talk
,
#1

In this lecture we look at how to add vectors together, which is one of the more common things you’ll be doing with two vectors.

For your challenge, I want you to find the current position of a camera that’s following the player at a fixed distance.

The player starts at (5,0) and the camera starts at (2,1).

First find the offset between the player and the camera.
Then work out the camera position when the player has moved to (11,0).

Once you’ve found your answers, post them below to let us know how you got on (remember to use spoiler tags).

If you need some extra help, there are some extra hints at the end of the video.

#2

new camera pos is at (8,1)

1 Like
#3

The offset is (-3,0)
When you put in the values you get (8,1) as the new camera position.

Here is the math:

CameraPos - PlayerPos = offset

(8,1) - (11,1) = (-3,0)

Now to check

PlayerPos + offset = CameraPos

(11,1) + (-3,0) = (8,1)

I’m not going to lie I was confused but I think I figured it out. I was just unsure how we used the hints to help get the offset. Instead I just counted the starting point where we had the player at (5,1) and the camera at (2,1) and did the same when it was at (11,1), but I felt like I didn’t really do anything special.
@garypettie I think i’m just overthinking it.

#4

Hey @Kevin-Brandon ,
When you draw the problem out like this, it’s pretty easy to get the answer just from looking at it and thinking it through.

If you were just starting with the two variables and no picture, it’s a little more abstract.
Say you just had the two variables in code:
playerPos = (5,0)
cameraPos = (2,1)

This is where finding the offset and storing it in a variable can be useful.
So you can do a vector subtraction to get;

offset = cameraPos - PlayerPos
offset = (2, 1) - (5, 0)
offset = (2-5, 1-0)
offset = (-3, 1)

And now you can just add that offset to the player, where ever they may end up.

So at (11,0) it would be;

cameraPos = playerPos + offset
cameraPos = (11, 0) + (-3, 1)
cameraPos = = (11-3, 0+1)
cameraPos = = (8, 1)

or if the player was at say (-5, 3), you’d get;

cameraPos = playerPos + offset
cameraPos = (-5, 3) + (-3, 1)
cameraPos = = (-5-3, 3+1)
cameraPos = = (-8, 4)

Hopefully that helps clear things up. If not, do let me know.

3 Likes
#5

This is exactly what I needed. Thank you Gary! Now I understand completely. My least favorite thing in math is getting the right answer but not completely understanding how.

3 Likes
#6

Calculating the camera offset always gave me a hard time when I’m trying to get the camera to follow the player because I keep forgetting which Vector should be subtracted from the other :sweat_smile:

20201001_131155
20201001_1311554032×2268 251 KB

1 Like
#7

I did screw this up a bit at first and subtracted camera from player (which gave the inverse of the vector I was looking for. The answer was obviously wrong (-3, 1), but figuring out which vector to subtract from is definitely something I need to wrap my head around. I’m going to watch the hints next and read through previous posts to see if it’s already come up! I just wanted to post my answer before I read any more.

Camera − Player = ((2−5),(1−0))
Camera −Player=(−3, 1)=CameraOffset

〖Player〗_1+CameraOffset=((11+(−3)), (0+1))
〖Player〗_1+CameraOffset=(8, 1)

1 Like
#8

@Dendrolis, you’re spot on!

#9

The offset will be (-3, 1), which is camera position (2, 1) - player position (5, 0). The camera position after player has moved will be (8, 1), which is either new player position (11, 0) + offset (-3, 1) or old camera position (2, 1) + movement of player (6, 0). (

#10

camera = (2, 1)
player = (5, 0)
offset is then = (-3, 1)
player goes to (11, 0)
camera will be (8, 1)

1 Like
#11

the offset is (-3,1) camera offset is (8,1)

#12

(11,0) + (-3, 1) = (8, 1)

#13

I found the offset to be (-3,1)

Therefore, when the player is at (11,0), the camera is at (8,1)

#14

Hi I got a different result because I don’t understand why the player vector is treated as the second vector. If treated as the first the result yields a different offset.

Player vector (5,0)
Camera Vector (2, 1)
Offset = (5-2, 0-1) = (3, -1)

When the player is at (11, 0) I get the camera at (8, 1). by substracting the offset again.

I don’t understand how do you decide which vector is vector 1 and which one is vector 2 when performing the subtraction. Deciding wrong seems to alter the result.
I also don’t understand why you add the offset to the player position once it changes instead of substracting it. I substracted it and got (8,1) which seems to be the answer but I am not sure if I got to it in the correct way. I would have gotten (14, -1) if I would have added it which seems completely off.

#16

Hello, Alejandro. I know it’s kinda late and I’m not the instructor, but I totally get why you are confused, because it doesn’t seem that clear to me as well.

I’d recommend thinking about the problem as not substracting the Player’s vector, but adding the negative Player’s vector, because the Camera is lagging behind the Player, and though both the Camera and the Player move from the origin point of 0;0, the direction of the movement from the Player to the Camera is negative (the Player would have to move back to reach the Camera). I’m not sure if that’s the right way to explain it, but this is how I understood this whole thing myself, hope it helps.

1 Like
#17

To get the vector we just subtract (2,1) from (5,0),obtaining the vector (3,-1)

After translating we just subtract (3,-1) from (11,0) obtaining (8,1) for the camera position

1 Like
#18

The player will bet at (5,0)

The camera will be at (2,1)

Offset (2 - 5), (1 – 0)

Offset -3, 1

New Player position (11, 0)

(11, 0) + (-3 +1)

(8,1)

1 Like
#19

Camera offset = (2-5, 1-0) = (-3,1)

New Player Position + Offset = Camera Position
Camera Position = (11 , 0) + (-3 , 1) = (8 , 1)

1 Like
#20

Player = a, Camera = b.

Start Position: a=( 5, 0 ), Camera b=( 2, 1 ), ||ab|| = √((5-2)² +(0-1)²) = 3.16

Player moves ( 6, 0 )

New Position: a=( 5 + 6 = 11, 0 ), b=( 2 + 6 = 8, 1 ), ||ab|| = √((11-8)² + (0-1)²) = 3.16

#21

The inital offset vector is (-3,1) so if the player is now at (11,0) the camera will be at (8,1)

Privacy & Terms