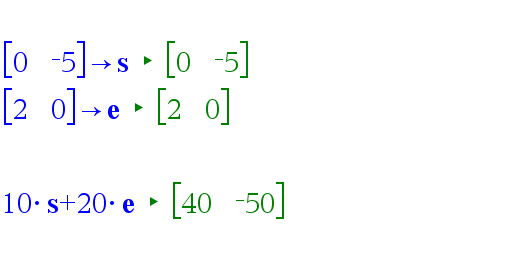Math - Scalar Multiplication

[garypettie]

In this lecture we look at scalar multiplication and how it can be used to alter the movement speed of the player.

For your challenge, we want to find out where the player will end up after a fixed set of instructions:

1. The player starts at (0, 0)
2. The player moves south (0, -1) at 5 units/second for 10 seconds
3. The player moves east (1, 0) at 2 units/second for 20 seconds
4. Where did they end up?

For some additional hints, watch to the very end of the video.

Once you’ve got your answer, post your answer below and remember to use the spoiler tags.

[EddieRocks]

(-50,40)

[garypettie]

@EddieRocks, almost but not quite. Double check the order of your elements.

[EddieRocks]

oops… gotcha… just did it in order not paying attention to direction

[garypettie]

happens to the best of us!

[Kevin-Brandon]

I got (40,-50)

[Ajai_Raj]

Start at (0,0)

Move south at 5u/s for 10s = Move down on the y axis 50 units = (0, -50)
Then move east at 2u/s for 20s = Move right on the x axis 40 units = (40, -50)

The player ends up at (40, -50)

[Dendrolis]

1). StartPos = (0, 0)
2). PlayerVelocity1 = (0, -5)
- Scalar = 10 (seconds)
- 10(0, -5) = (0, -50)
3). PlayerVelocity2 = (2, 0)
- Scalar - 20 (seconds)
- 20(2, 0) = (40, 0)
4). StartPos + PlayerVelocity1 + PlayerVelocity2 = EndPos
- (0, 0) + (0, -50) + (40, 0) = (40, -50)
EndPos = (40, -50)

[Joshzerogod]

SOUTH velocity is (0, -1) and the south speed is 5 u/s, which gives us (0, -5). The time he is moving SOUTH is 10 s, which has to be multiplied with the vector (0, -5) resulting in the SOUTH vector (0, -50).
EAST velocity is (1, 0) and the east speed is 2 u/s, which gives us (2, 0). The time the player is moving EAST is 20 s, which has to be multiplied with the vector (2,0) resulting in the EAST vector (40, 0).
Adding now the SOUTH and EAST vector results in (0, -50) + (40, 0) = (40, -50).
So the player ends up at (40, -50).

[Jeff_Simon]

a = 10 (0,-1(5))
b = 20 (1*(2),0)
a + b = (40, -50)

[DefectiveButCaring]

->
player = (0,0)
->
southmovement = (0, -1) * 5
->
southmovement = (0, -5)
-> -> ->
player = player + (southmovement * 10)
->
player = (0, -50)
->
eastmovement = (1, 0) * 2
->
eastmovement = (2, 0)
-> -> ->
player = player + (eastmovement * 20)
->
player = (40, -50)

[archbishopFPP]

One of my favorite classes in college was Statics, the first time I saw the practical application of vector math. As such, I think of vector magnitude as a physical force being applied to an object (in this case, the player).

So…for the first 10 seconds there is a -vertical force of -50 and a +horizontal force of 20. Add those two vectors: (0, -50) + (20, 0) = (20, -50). This is the player’s position at 10 seconds.

For the next 10 seconds there is only the +horizontal force of 20. Add this to the player’s last position: (20, -50) + (20, 0) = (40, -50).

This certainly works, but for coding’s sake I need to develop the habit of starting with unit vectors and multiplying by the scalar. The brain is great at inference; a computer, not so much.

[Mikapo]

Here is mine:

[u571989]

player moves south (0,-1) * (510)= (0,-50)
player moves east (1,0)(2*20)=(40,0)
player position is (40,0)+(0,-50)=(40,-50)

[Gianni]

1. The player moves south (0, -1) at 5 units/second for 10 seconds

(0, -50)

2. The player moves east (1, 0) at 2 units/second for 20 seconds
   Where did they end up?

(40, -50)

[TheSnooze]

Hey Gary!

Here’s my solution and I hope I type this out correctly:

(0, -5) * 10 = (0, -50)
(2, 0) * 20 = (40, 0)

So the final coordinate would amount this way:

(0, 0) + (0, -50) + (40, 0) = (40, -50)

[Kbot]

(40, -50)

[Giovanni]

You just need to add (0,-50) and (40,0) to get the vector (40,-50)

[Stephen_Aho]

South (0,-1) Times the Scalar (50) = (0,-50)
East (1,0) Times the Scalar (40) = (40,0)

South + East = (0,-5-) + (40,0) = (40,-50)

[sandninja]

Move (5*10) = 50

South = (0, -1)

*50 *50

Move 1 = (0, -50)

Move (2 * 20) = 20

East = (1, 0)

*20 *20

Move 2 = (40, 0)

Move 1 = (0, -50)

• Move 2 = (40, 0)

= (40, -50)