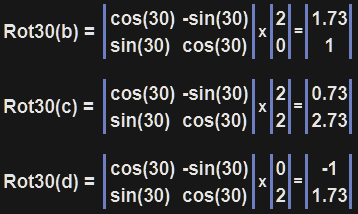In this lecture we looked at how to build a rotation matrix to help us rotate our objects in 2D.
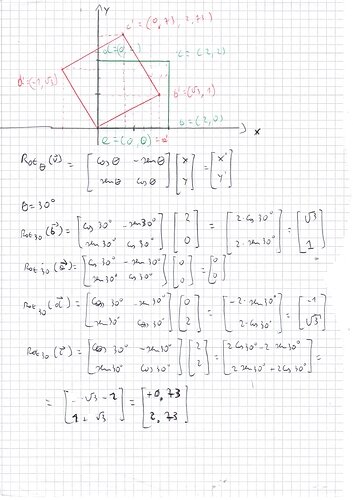
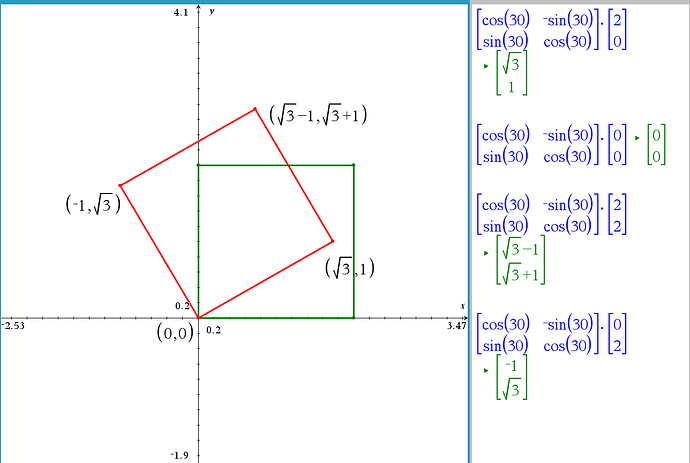
For your challenge we were trying to rotate a box by 30 degrees.
This box had it’s vertices at points; (0, 0) || (2, 0) || (2, 2) || (0, 2)
Did you manage to find where each point ends up after applying the rotation matrix?
Post your answers below and remember to use the spoiler tags.
I feel like I did something wrong, but I got:
a = (0,0)
c = (1.23, 2.73)
d = (1, 3^1/2)
I got D by flipping the coordinates for B, but then I switched the sign of x to get (-1, 3^1.2) because x clearly has be be negative.
Did I miss something? I went back to review how to get the dot product, but maybe I miscalculated somewhere?
Hi @Ajai_Raj, apologies for the very late reply (my original response didn’t post for some reason).
You’re almost there but it looks like you might have gotten a little lost in places.
Here’s the full solution so you can check your calculations:
a' = (0,0)
b' = [cos30 -sin30] [2]
[sin30 cos30] [0]
b' = [cos30 • 2 + (-sin30) • 0]
[sin30 • 2 + cos30 • 0]
b' = (√3, 1)
c' = [cos30 -sin30] [2]
[sin30 cos30] [2]
c' = [cos30 • 2 + (-sin30) • 2]
[sin30 • 2 + cos30 • 2]
c' = (√3 - 1, √3 + 1)
d' = [cos30 -sin30] [0]
[sin30 cos30] [2]
d' = [cos30 • 0 + (-sin30) • 2]
[sin30 • 0 + cos30 • 2]
d' = (-1, √3)
a = (0, 0)
b = (1.73, 1)
c = (0.73, 2.73)
d = (-1, 1.73)
This is what I got:
the three new points (with √3 converted to 1.73) are
(1.73, 1)
(.73, 2.73)
(-1, 1.73)
a=(0,0)
b=(√3,1)
c=(√3-1, 1+√3)
d=(-1,√3)
(0, 0) => (0, 0)
(2, 0) => (sqrt 3, 1)
(2, 2) => (sqrt 3 - 1, sqrt 3 + 1)
(0, 2) =>(-1, sqrt 3)
a) (0 , 0)
b) (1.732 , 1)
c) (0.732, 2.732)
d) (-1, 1.732)
original x orginal y rotated x rotated y
0 0 0 0
2 0 1.732050808 1
0 2 -1 1.732050808
2 2 0.732050808 2.732050808
a = (0; 0)
b = (cos30 * 2; sin30 * 2) = (1,73; 1)
c = (2cos30 - 2sin30; 2sin30 + 2cos30) = (0,73; 2,73)
d = (-2sin30; 2cos30) = (-1, 1,73)
a = (0, 0)
b = (√3, 1)
c = (0.73, 2.73)
d = (-1, √3)
