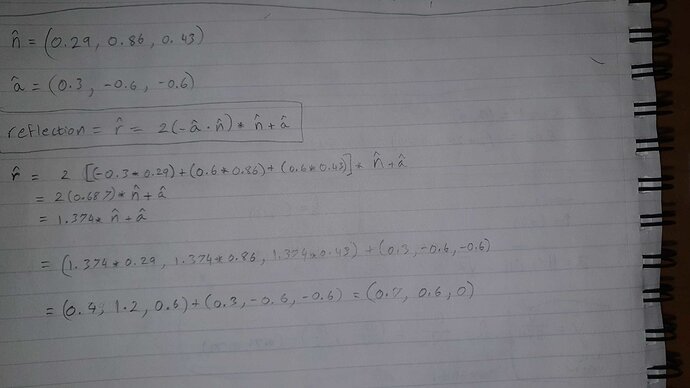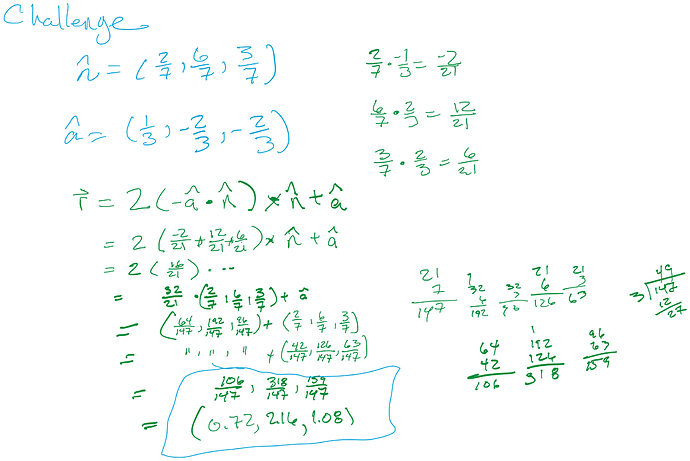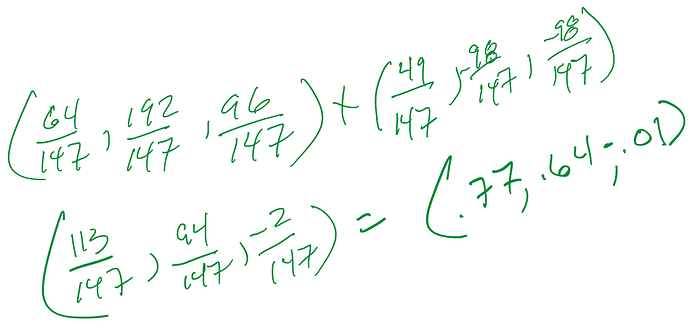In this lecture look at how to reflect (or bounce) an object off of a surface.
For you’re challenge, I gave you the normal vector of a surface and the direction of the incoming object.
n = (2/7, 6/7, 3/7)
a = (1/3, -2/3, -2/3)
Did you manage to find the reflection vector? Post you answers below and remember to use the spoiler tags.
Brain struggling so definitely not convinced but here’s tonights answer…
0.77, 0.69, -0.01
Very close @EddieRocks.
Your x- and z- values look correct but your y- value is slightly off.
It could just be a typo though, so do the final addition step again and see if the mistake is just cropping up at the end there.
I make the answer:
(113/147, 94/147, -2/147)
or
(0.769, 0.639, -0.014)
Here are the full calcs (using fractions so I can do it by hand):
r = 2(-(1/3, -2/3, -2/3) • (2/7, 6/7, 3/7)) x (2/7, 6/7, 3/7) + (1/3, -2/3, -2/3)
r = 2(16/21) x (2/7, 6/7, 3/7) + (1/3, -2/3, -2/3)
r = 32/21 (2/7, 6/7, 3/7) + (1/3, -2/3, -2/3)
r = (64/147, 192/147, 96/147) + (1/3, -2/3, -2/3)
r = (64/147, 192/147, 96/147) + (49/147, -98/147, -98/147)
r = (113/147, 94/147, -2/147)
r= (0.769, 0.639, -0.014)
yes twas a typo - cheers
My fractions came out gnarly so I’m not at all confident in this, but:
(85/147, 150/147, 54/147)
@Ajai_Raj, the fractions in the answer do look pretty unfriendly so don’t always expect the answers to be nice and tidy (they rarely are unless you pick very specific values to work with).
You’re denominator of 147 is correct, but it looks like you’ve gone wrong somewhere when working through your solution.
You can check your calculations against my spoiler post above to see where you went wrong.
Or if you share your full calculation I can point you in the right direction.
Sure thing:
r = 2 ( (-1/3 * 2/7) + (2/3 * 6/7) + (2/3 * 3/7) * n + a
= 2(-2/21 + 12/21 + 6/21) * n + a
= (-4/21 + 24/21 + 12/21) * n + a
= 32/21 * (2/7, 6/7, 3/7) + a
= (64/147, 192/147, 96/147) + (49/147 , -98/147, -98/147) <- This is where I went wrong, I scaled the fractions in vector a wrong
= (113/147, 94/147, -2/147)
= the correct answer?
@KhaledAhmedYounes, great work.
You’re calculations look fine but you’ve introduced some small rounding errors.
Be careful not to round your numbers too early and always work with a few extra levels of precision than you need for your final answer, so that they don’t stack up over time.
@Dendrolis, well done for giving this challenge a go, you were almost there but you made a small mistake right near the end.
On the 5th line, you’ve worked out all the tough stuff but then added n instead of a.
If you fix that then you should get to the correct answer (and yes the answer does have some fairly horrible looking fractions!).
Thanks. Of course it was a silly mistake. I figured it didn’t make sense for the answers to be more than 1 since we started with unit vectors but I missed where I went wrong. I was looking at all the initial calculations.
My reflection vector r is (0.77, 0.64, 0.39).
Just found an error in my calculation. The reflection vector r should be (0.77, 0.64, -0.01) instead of (0.77, 0.64, 0.39).
->
r = (0.77, 0.64, -0.02)
@DefectiveButCaring, great work. This is a difficult challenge! 
It looks like you’ve got the correct answer, just be careful with your rounding.
The z-component should be -2/147 or around -0.0136, so when you round it off you should end up with -0.01.
Oh yea, I messed it up. Thank you for telling me, I will keep my eyes opened to not do that again.
I got it wrong the first time, tried again and came up with the answer.
N = (2/7, 6/7, 3/7)
A = (1/3, -2/3, -2/3)
Reflect it
R = 2(-A . N) * N + A
R = 2(-2/21 + 12/21 + 6/21) * N + A
R = 2(16/21) * N + A
R = 32/21 * (2/7, 6/7, 3/7) + A
R = (64/147, 192/147, 96/147) + (1/3, -2/3, -2/3)
R = (64/147 + 49/147, 192/147 - 98/147 , 96/147 - 98/147)
R = (113/147, 94/147, -2/147)
