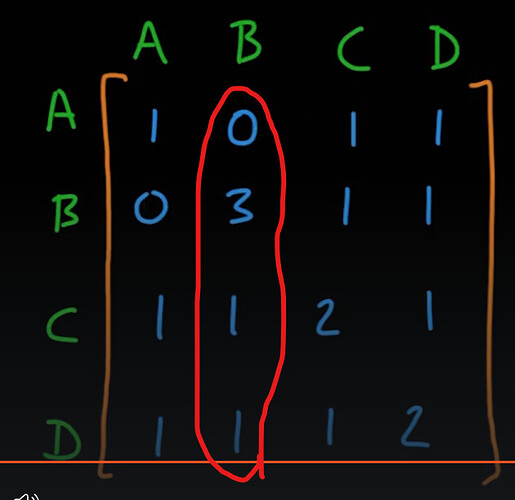
In this lecture we learnt how to multiply two matrices together and looked at how this can be useful when combined with what we learnt about the adjacency matrix in the last lecture.
Did you manage to find the cube of our original adjacency matrix, and so find how many paths exist between two nodes that take exactly 3 steps?
var t = matrix1 * matrix2;
print(t.m00 + " " + t.m01 + " " + t.m02 + " " + t.m03);
print(t.m10 + " " + t.m11 + " " + t.m12 + " " + t.m13);
print(t.m20 + " " + t.m21 + " " + t.m22 + " " + t.m23);
print(t.m30 + " " + t.m31 + " " + t.m32 + " " + t.m33);
0—3---1----1
3—2---4—4
1—4---2—3
1—4---3—2
i used Unity
A B C D
A 0 3 1 1
B 3 2 4 4
C 1 4 2 3
D 1 4 3 2
I don’t get how we do find how many paths exist between two nodes in the result.
The Matrix itself shows this. It is the sum entries in a given column. So, for Node B (the second column) as an example, there are 3 connections and only B connecting to B is zero. This of course is when you’re dealing with a single connection.
When specifying n=2, this would become 5 as there would be because B can connect to itself by going to A, C or D and back to B but can no longer connect to A because there is no valid 2-step path to B to A.
I hope this helps
It totally helped! Thanks for the explanation
