In this lecture we learnt how to alter the amplitude and frequency of our standard sine wave and also looked at how to move the curve on the x- and y- axes.
We applied our modified curves to the head of a turret and to a blinking light, but you can apply them to pretty much anything.
What are some of your favorite uses of the sine wave?
Before this lecture I would have said my favorite use for sine waves was moving platforms (except I wouldn’t have actually known sine waves were involved per se). Now I think turret range of motion is a cooler application, but I really love them both.
Also, does this apply in 2D as much as in 3D? If I wanted to make a platformer with moving platforrms and turrets, I could implement and manipulate them using sine waves?
You can absolutely use them in 2D. In fact, all the math we covered was looking at sine waves from a 2D perspective.
If you think about a platform that moves horizontally back and forth, you’re only moving it on the 1 axis, so it makes no difference whether you’re working in 2D or 3D.
The only functionality you really lose in 2D vs 3D is something that we didn’t actually cover in the lecture, and that’s the ability to make spirals.
Here’s a nice diagram that that shows what I’m talking about:
Oh, that’s super cool. Are there any good online resources that break this down? Would be awesome to implement this in a game.
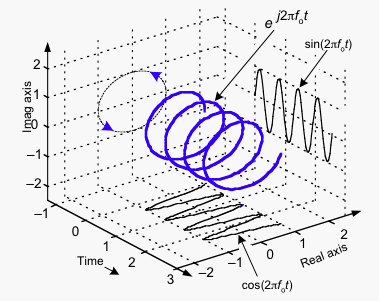
That image actually makes it look way more complicated than it really is.
If you ignore all the fancy formulas and math terms, it’s really just a logical extension of what we looked at in previous lectures.
We know that, as you move around the circumference of a circle, you’re changing the x-coordinate by cos(theta) and the y-coordinate by sin(theta).
Now, to turn the circle into a spiral, you just need to start moving it forward.
So if you also increase your z-position at a constant rate, you’ll end up stretching out that circle into a spiral.
This is why you can do it in 3D but not in 2D. You need that third dimension in order to push the circle forward and turn it into a spiral.
I have a background in theatrical lighting, and most of the effects in the consoles are built on sine waves. You use them to build pan/tilt effects on moving heads/ color effects by cycling/offsetting RGB channels in LED fixtures and controlling the amplitude and x/y offset to control the start end values. I’ve literally created the same thing as used in the flashing light example to control color, then run a sequence of those lights on a sine wave for intensity as well to create a chase (either for something like marquee lights or for an effect like windows on a train). The naming is different, but the idea is the same.
Hi I am having an issue understanding how is it that you figured out the amount that you needed to add in order to swift the sine wave on the x axis. I understand why 1/2 was added in order to swift the sine wave on the Y axis and avoid it from going below 0 and actually getting to 1. On the example you used t/4 for subtraction and 3t/4 for addition to swift the sine wave on the x axis. How did you figured these where the necessary values to add?
Great question @Alejandro_Borge1!
The first thing to remember is that there are Ď„ radians in a circle.
Secondly, each cycle of the sine wave is one revolution around the circle.
Therefore, each cycle of a sine wave moves through Ď„ radians.
From the graph we have at ~7:20, you can see that the sine wave is at y = 0 around 3/4 of the way through its cycle.
So, to move the wave into the position we want, we can either; subtract 3Ď„/4, or add Ď„/4.
I hope that helps
Greetings, Everyone!
As I can see, there is not much activity in discussions long after the course was published, but for those, who is learning long after (like me) I consider that pluralism of thoughts has its benefits.
You can find an interesting implementation of waves in “Sea of Thieves” - at least you can check the short video (3min) about physics behind the sea waves, by searching “how water works in Sea of Thieves” on YouTube.
Hope, that somebody will find it helpful.
Thanks for your time.
I found this lecture/section too fast. In particular, the challenge of the light. The parts needed were covered very quickly and not very well illustrated on the graph. In particular the part about “changing the angle” which in the given equation was the xOffset (but not explained as such at all). Also, we haven’t all internalized that tau represents a full circle, so the explanation really needed to slow down and remind us why we used tau/4 or 3tau/4 visually by overlaying or sliding the wave left or right.
Overall this section was really poor compared to the rest of the circle/triangle stuff that led up to it, which I have found thorough and patient.
