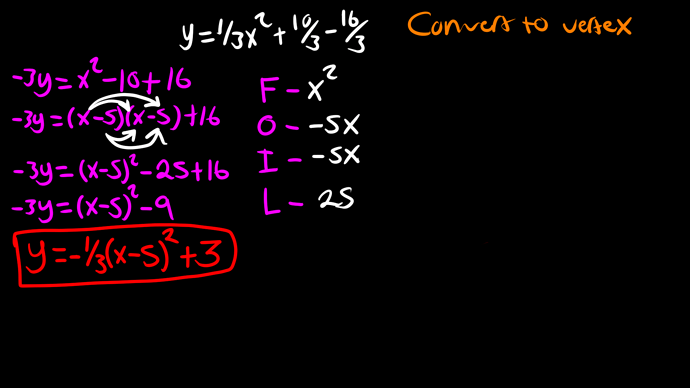This reciprocal stuff broke me. I had to watch an hour of YouTube explainers. I still don’t get it. lol
Challenge:
y = (-x^2 + 10x - 16) / 3
y = (-1/3)x^2 + (10/3)x - (16/3)
(R) = -3
-3y = x^2 - (30/3)x + (48/3)
-3y = x^2 - 10x + 16
-3y = (x - 5)^2 - 25 + 16
-3y = (x - 5)^2 - 9
y = ((x - 5)^2 - 9) / (-3)
y = (-1/3)(x - 5)^2 - 3
My answer to the Completing the Square challenge:
Q1. Given y = (-1/3)x² + (10/3)x - (16/3), convert to vertex form
A1. y = (-1/3)(x - 5)² + 3
A1a. y = (-1/3)x² + (10/3)x + (16/3)
A1b. -3y = x² - 10x + 16
A1c. -3y = (x - 5)² - 25 + 16
A1d. -3y = (x - 5)² - 9
A1e. y = (-1/3)(x - 5)² + 3
Is this correct? I struggled with this one quite a bit, ultimately i found out the problem was i kept making it -3y = (x-5)^2 + 25 - 16, but i still cant figure out why -5 * -5 ends up as a -25 in the equation?
This took me a while of studying the example and making sure I got the formulae right. I keep messing up the negatives … need to work slower!
I ended up with: y = -1/3(x - 5)^2 + 3 which puts the vertex at (5,3)
Welcome to the community. I assume the bullet was originally a negative sign?
