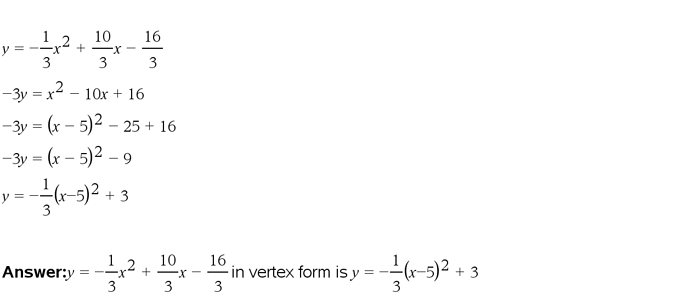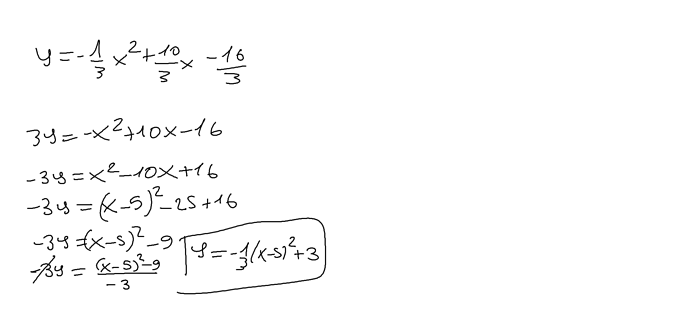I’m glad I could help.
Be sure to keep asking questions whenever something doesn’t quite make sense, and I’ll happily provide extra details if I can.
y = (-1/3)(x^2) + (10/3)x - (16/3)
-3y = (x^2) - 10x + 16
-3y = ((x - 5)^2) -25 + 16
-3y = ((x - 5)^2) -9
y = (-1/3)((x-5)^2) + 3
vertex is (5,3)
My results:
y = -1/3x² + 10/3 - 16/3
-3y = x² - 10 + 16
-3y = (x - 5)² - 25 + 16
-3y = (x - 5)² - 9
y = -1/3(x - 5)² + 3
Vertex is (5,3)
y = -1/3(x-5)^2 + 3
the equation is y=(-1/3)(x-5)^2+3
the vertex coordinates are (5,3)
y = -1/3(x - 5) + 3
This one had me struggling for a while, but I understand why we did the square and the b/2 much better now , this is how it played out:
y = -1/3^2 + 10/3x - 16/3 which I know is y = ax^2 + bx + c so a = -1/3 b = 10/3 and c = -16/3
to simplify * -3 so -3y = x^2 + (-10) + 16
The formula for completing the square is y = (x + b)^2 - b and we need to ad c so
-3y = (x + (-10/2))^2 -(10/2)^2 + 16
-3y = (x -5)^2 - 9
y = -1/3(x-5)^2 + 3
Here is the conversion :
-3y = x^2 - 10x +16
-3y = (x-5)^2 - 25 +16
-3y = (x-5)^2 - 9
y = -1/3(x-5)^2 + 3
Vertex = (5,3)
This is actually the first time during this course I struggled a bit. I googled around on ‘Factoring Perfect Square Trinomials’ and found another method which made this easier to understand and calculate imo. So this is what I got:
Standard form:
y = -1/3x^2 + 10/3x - 16/3
My solution:
Factor our the -1/3:
y = -1/3(x^2 + 10x) - 16/3
To create a perfect square we need to divide b with 2:
(10/2)^2 = 25
Because I added 25 * -1/3 so I need to subtract 25 * 1/3 outside the parenthesis:
y = -1/3(x^2 + 10x + 25) - 25 * (-1/3) - 16/3
Calculate c:
-25 * (-1/3) - 16/3 = 3
Factoring perfect square trinomials pattern: (a−b)^2 = a^2 - 2ab + b^2
√25 = 5
√x^2 = x
2 * x * 5 = 10x
So it would be: (x - 5)^2
Answer:
y = -1/3(x - 5)^2 + 3
Starting with y = -1/3 x^2 + 10/3x - 16/3, here’s what I got:
-3y = x^2 - 10x + 16
-3y = (x-5)^2 - 25 + 16
-3y = (x-5)^2 -9
y = -1/3(x-5)^2 + 3
y = -1/3x^2 + 10/3x -16/3
Convert to Vertex Form:
-3y = x^2 - 10x + 16
-3y = (x + 5)^2 - 25 + 16
-3y = (x + 5)^2 - 9
y = -1/3(x - 5)^2 + 3
Good morning!
Here is what I did
y = - 1/3x^2 + 10/3x - 16/3
-3y = x^2 - 10x + 16
= [ (x + ( -5 ))^2 - ( -5 )^2 ] +16
= [ (x - 5)^2 - 25 ] +16
-3y = (x - 5)^2 - 9
Vertex Form is
y = -1/3 (x - 5)^2 + 3
Coordinates (-5, 3)
x should not be negative here. I made a mistake but my signs seem correct
I can copy along with other peoples answers and can get the answer but I don’t really understand this one, I think the lesson glosses over things and isn’t great for people who don’t already have an in depth knowledge of algebra. This is my 5th gamedev.tv course and I think you guys are great but you always get to this quarter point and it seems you take the training wheels away and get on with it. On the other courses it wasn’t so bad but this left me watching the video over and over without getting it fully.
I have tried switching the X out with a number and for me it doesn’t add up but maybe I’m just being a dummy. Anyway here is my answer.
Y = (-x^2 + 10x -16)/3
3y= -x^2 +10x -16
We then remove the - from the x^2 ( where have we been taught to do this? I feel like I missed something.
-3y= x^2 -10x +16
-3y= (x + 5)^2 - 5^2 +16
-3y= (x+5)^2 -25 +16
-3y= (x+5)^2 -9
y= -1/3➗(x+5)^2 +3.
i get
y=-1/3(x-5)^2 +3
y=-(1/3)x^2+(10/3)x-16/3 =>
-3y=x^2-10x+16=(x-5)^2-25+16=(x-5)^2-9 =>
y=-(1/3)*(x-5)^2+3
y = -1/3 (x-5)^2 + 3
The main hurdle is to convert x^2 - 10x into (x - 5)^2 -25 (we nullify the -5^2 by substracting -25)
y = -1/3 x^2 + 10/3 x - 16/3
-3y = x^2 - 10x + 16
-3y = (x - 5)^2 - 25 + 16
-3y = (x - 5)^2 - 9
y = -1/3 (x - 5)^2 + 3
y = -1/3x^2 - 10/3x + 16/3
-3y = x^2 - 10x + 16
-3y = (x - 5)^2 - 25 + 16
-3y = (x - 5)^2 - 9
y = -1/3(x - 5)^2 + 3