In this lecture we looked at how to find the mean, median, and mode of various datasets and discussed some of the pros and cons of each.
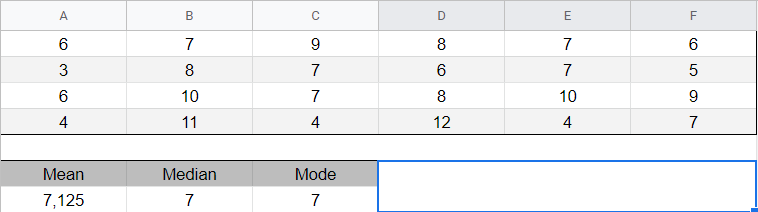
For your challenge, you were asked to find the mean/median/mode of the dataset:
{6, 7, 9, 8, 7, 6, 3, 8, 7, 6,7 5, 6, 10, 7, 8, 10, 9, 4, 11, 4, 12, 4, 7}
Post your answers below and remember to use the spoiler tags!
Here are the answers so you can check them against your own.
Mean:
The mean is the average that most people think of first.
To find it, add all of the values in the dataset and divide by the count.
171 ÷ 24 = 7.125
Median:
The median is the “middle” value.
To find it, just order your dataset and then find the value in the middle.
In this case we have an even number of values, so the median sits between elements 12 and 13.
Fortunately these are both 7, so the median is also 7… (7+7) ÷ 2 = 7
Mode:
The mode is the most common value in our dataset.
To find it, place your values into a frequency table and see which one is most popular.
For us, this is the number 7.
mean: 7.125
median: 7
mode: 7
mean 7.125
median 7
mode 7
Python 2 median solution
list = [6, 7, 9, 8, 7, 6, 3, 8, 7, 6, 7, 5, 6, 10, 7, 8, 10, 9, 4, 11, 4, 12, 4, 7]
list.sort()
length_of_list = len(list)
if length_of_list % 2 == 1:
print(list[(length_of_list / 2) + 1])
else:
print((list[length_of_list / 2] + list[length_of_list / 2 + 1]) // 2)
7.125 is the mean
7 is both the median and the mode
The mean is 7.125
The median is 7
The mode is also 7
| sum | 171 |
|---|---|
| count | 24 |
| mean | 7.125 |
| median | 7 |
| mode | 7 |
mean = 7.125
median = 7
mode = 7
Mean = 171/24 = 7.125
Median = 7
Mode = 7
