I am coming from zero math and making this made me so thankful. Please continue teaching with real life examples.
4 Likes
@ontendo great job, I might have missed this.
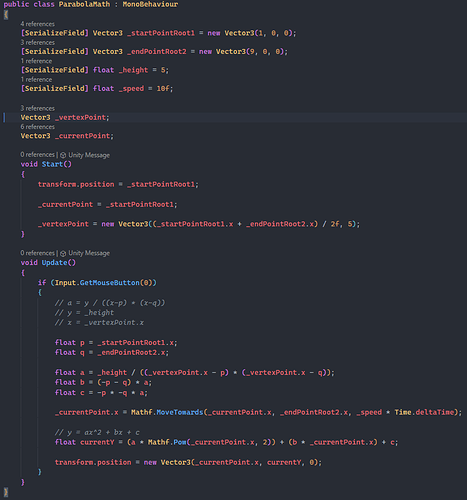
I was just curious how did you evaluate the equation for
b = (-p -q) * a
c = -p * -q * a
I am trying to wrap my head around it
2 Likes
I don’t remember quite clearly because I gave names depending on the video. I have to watch the video again for that. I was just doing how this c or b can be found from other values like what is the relation.
1 Like
formulae of parabola
Standard: y = ax^2 + bx + c
Interception: y = a(x-p)(x-q)
Vertex: y = a(x-h)^2+ k OR x = a(y-k)^2+h
I am not sure how you substituted or came up with
b = (-p -q) * a
c = -p * -q * a
When ever you remember do share it, It would be a great help
thank you. ;-D
2 Likes
Hey Splunky,
I can give you the answer.
You can deduct those formulas from y = a(x-p)(x-q).
When you go back to the standard formula you do the following steps using FOIL method:
y = a(x^2- qx - px - p * - q)
y = ax^2 -aqx -apx + a(-p*-q)
then you can say, because x is a common factor in -aqx -apx
y = ax^2 + x(-aq - ap) + a(-p * -q)
If you pay attention to this, you can notice that (-aq - ap) is just a number and we can call this b and a(-p* -q) is also a number you can call this c.
Going back to your question we can say that:
b = (-aq - ap)
a is a common factor then you end with
b = a * (-q -p)
And
c = a (-p * -q)
I hope I was clear, if you have any other questions don’t hesitate to ask.
2 Likes