I did try to get an inverse matrix on my own and here is the result
I think I understand how to do this now. It’s really time-consuming to do it like this. But I am really happy I got it right because the matrix is completely new for me. I am kinda surprised that it was not taught when I was in high school.
I have also a question. How is the inverse matrix useful for game developing?
oh wow this must have taken you awhile.
I actually wondered that myself. I’m sure @garypettie can help.
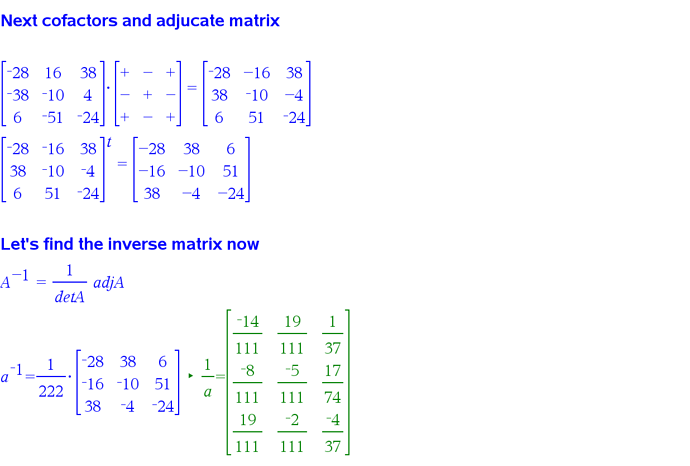
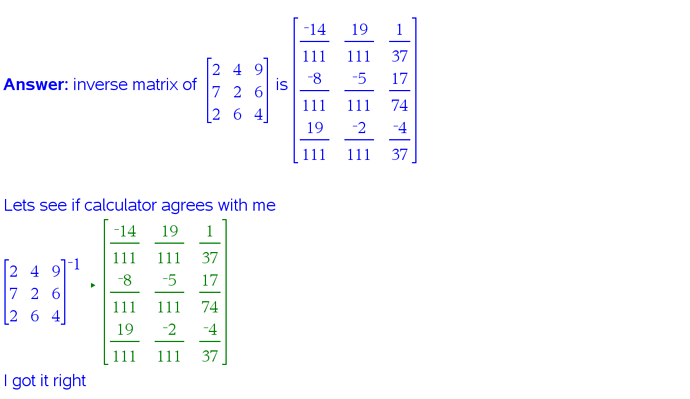
Great work @Mikapo!
I agree that it is quite a long and laborious task to complete by hand, but it definitely gives you a deeper appreciation for the relationship between a matrix and its inverse.
You can use it for all sorts of calculations. Any calculation that involves multiplying two matrices can be “undone” with the matrix inverse.
In practice, matrixes are used heavily in graphics processing, so if you ever start messing about with more complex graphical or compute shaders then you’ll almost certainly run into them.
They’re used heavily for the things like object transformation, rotation and scaling but luckily game engines do a good job at shielding us from a lot of the complexity.
As a simple example, one way to change the direction of rotation would be to multiply your vector by the inverse rotation matrix.
Thank you for your response. Sorry if I bother you with this but could you show an example of how you can undone matrix multiplication with the matrix inverse? I would be interested to learn this.
All you need to do is use the formula I mentioned in the video.
If you have A * B = C then you can say that B = A^(-1) * C
As a simple example, let’s look at rotating the point (2,0) by 30°.
[cos(30) -sin30] * [2] = [√3]
[sin(30) cos30] [0] [ 1]
Now let’s say that we have the final rotation and we want to know where it came from, given that we know it was rotated by 30°.
We can say use our result and the inverse rotation matrix to rotate clockwise back to the original point;
[cos(30) -sin30]^(-1) * [√3]
[sin(30) cos30] [ 1]
= [ cos(30) sin30] * [√3]
[-sin(30) cos30] [ 1]
= [2]
[0]
Obviously, this is a fairly contrived example, because rotation matrices have some other interesting properties - You could instead just throw in -θ and get the same clockwise rotation.
However, this (hopefully) gives you a sense of how the matrix inverse could be used when it comes to undoing any matrix multiplication. It’s really just the matrix equivalent of using division in regular algebra.
I understand now how it works and I can see how it can be useful in game developing. I likely will not need it for while until I try something more advanced but I will know how to use it when I need it. Thanks for your response it did really help.