I have a have a ball with a rigidbody attached and I am adding torque to the ball based on the angle of a third person camera (always looking at the ball) witch rotates around the ball. I am trying to change the direction of the ball based on the position of the camera in its rotation around the ball. I am using Vector3.right for forward and reverse torque and Vector3.back for right and left. I have the forward/reverse value, rightVal working but I have been working on the left/right value, backVal for three days and am at a loss. Here is how I am trying to accomplish this.
void CalcRightVal()
{
float degrees = Camera.main.transform.localEulerAngles.y;
if (degrees > 0 && degrees < 180.0f)
{
rightVal = (-degrees / 360) * 4 + 1;
}
if (degrees > 180.0f && degrees < 360.0f) //
{
rightVal = (-degrees / 360) * 4 + 1;
if (rightVal < -1.0f)
{
rightVal = (degrees / 360) * 4 - 3;
}
}
}
void ApplyTorque()
{
Vector3 dir = new Vector3(rightVal, 0, backVal);
ball.AddTorque(dir * ballAcceleration);
}
In ApplyTorque() I need the backVal to go from 0 to -1 i.e. Vector3.back when degrees == 90. Then backVal should increase in value to 0 when degrees == 180 then up to 1 when degrees == 270 then back to 0 when degrees == 360. This will apply torque to the right when the camera is at 90 degrees and left when the camera is at 270 degrees. The Idea is that the user will add input to forward i.e. KeyCode.W to add acceleration and reverse or KeyCode.S for breaks. The camera will be responsible for changing the direction of the force. I am not terrible at math but this one has me beat.
While rightVal is at 1 or -1, backVal needs to be at 0 and vice versa. That way when the camera is directly behind the ball or 0 degrees the torque applied will be Vector3.right or (1, 0, 0) and when the camera is at 90 degrees or on the left of the ball, torque applied will be Vector3.back or (0, 0, -1). This will apply torque to make the ball turn right. Basically wherever the camera is the ball rolls forward from the point of view of the user. Thank you for the help, and all help is always appreciated.
Here is a graphic to help out.
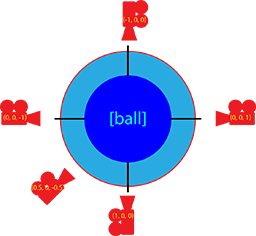
Thank You.

