Okay, let’s go back and look at this:
Let’s put some numbers here and pretend the collider size is 20 units across and 3 units large. Let’s also say the collider’s offset is (10, 1). If you were to click on a spot that had a world coordinate of 17,5, 3.25, and you subtracted the offset, you’d have a coordinate of (7.5, 2.5).
As a quick side example: To get a vector to someplace, you subtract it’s position from your current position. So, to go to a tree at tree.transform.position, my character would go to tree.transform.position - character.transform.position. This gets a vector from the character to the tree. From the character’s perspective, the character is at 0,0 and the tree’s coordinates are this vector.
So if the character is at (3, 7) and the tree is at (5, 9), then the vector between them is (2, 2). That is, from the character’s position, the tree is located two units high and two units to the right.
Now, going back to the grid, we have a position (the mouse click), and we are subtracting the position of the collider. Essentially, this is (click position - collider’s position), or a vector from the collider to the mouse click. If the mouse click is at 17,5 and the collider is located at 10,1, then when we subtract the collider’s position (the offset), we’re left with (7.5, 2.5). This is, from the collider’s perspective, the click is located 7.5 units to the right of the collider’s center and and 2.5 units higher than its center. These are essential the mouse click’s position at coordinates local to the collider.
That’s useful to us because we have a bunch of other coordinates local to the collider already, most notably it’s height and width. And if we know the height and width and number of rows and columns, then we also have the height and width of each grid cell.
Even just judging on the x-axis for the moment, there are (nearly) infinite number of spaces to click on from the left side of the collider to the right side of the collider. But there’s only seven spaces, seven distinct points that we care about. These are the center of our grid cells. Since they are evenly spaced throughout the collider’s width, we can determine what these points are by dividing the total width (20) by the number of cells along that axis (7). So basically, with any mouse result we get, we want to round to the nearest (20 / 7 = ) 2.857.
If we clicked on local x-axis position of 7.5, we can see that does not land on a perfect multiple of 2.857, so it has not landed perfectly on the grid. We can adjust this number by dividing by the width of a grid width (to see how many grid widths far away it is from the center) and get a result of 2.62513. That is, it’s gone exactly 2 full grid spaces to the right, and about 63% of another grid space. So when we “snap to grid”, we should be snapping to the 3rd grid space. So we round this 2.62513 result to 3, and then we multiply by the grid space.
If our grid coordinate at 0,0 is also the center of a cell grid at 0,0, then the center of the cell grid to the right is one full cell grid width away from the center. That is if the cell has a width of 2.857, then the grid position one space to the right should have an x coordinate of 2.857. Two spaces to the right should have a local coordinate of 5.714. Three to the right should have 8.571. That’s why we multiply the cell width when we convert back from grid coordinates to world coordinates. Since the number has been rounded to the nearest whole number, when we convert back, we should land perfectly in the middle of one of these spots.
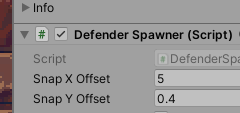
All of this assumes that 0,0 – the center of the collider – is also the center of a grid space, which does not appear to be true. You’ve already noticed the results – hence the need for a SnapXOffset and SnapYOffset. You need some sort of offset from the center of the collider to the center of a grid space.
The collider stuff kind of confuses things and adds some extra steps, but it’s useful for converting the picture into numerical data. My first thought would have been to use transforms, but it’s the same overall result. You need some way to get the width of a cell (cell size x), the height of a cell (cell size y), and the offset from 0,0 to the center of a cell. As long as you have those three pieces of information, you can make a grid by:
- Take a world position, and add the offset to it.
(This makes it a local position based on your starting cell.)
- Divide the x and y of your local position by the cell size x and y.
(This tells you far away the position is, in number of cells, in each axis)
- Round the x and y to whole numbers.
(This rounds the “distance in cells” to the nearest whole amount of cells, in each axis.). These are effectively your grid coordinates. (The number of cells horizontally and vertically from the starting grid space.)
- Multiply the distance by the cell size x and y.
(This converts the “grid coordinates” or “distance in cells from the center” back to the local coordinates of the starting grid cell. Remember these are not derived from the initial world position coordinates, but rather the coordinates of the center of the nearest cell.)
- Subtract the original offset.
(Converting back from local coordinates of the starting cell to Unity world coordinates (or distance from world origin 0,0). )







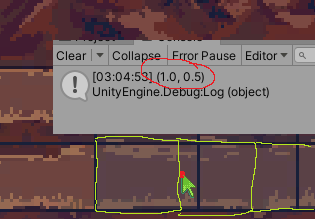

 i’ll update with further information, hoping i will solve it.
i’ll update with further information, hoping i will solve it. i’ll try to read better your response
i’ll try to read better your response