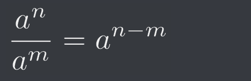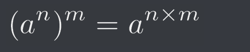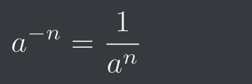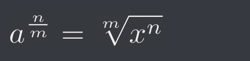How the X value was fully obtained?

[Daniel_Thorne]

I’m not sure if I am missing something, however, around 5:12 and 5:14 (I think) it kinda cuts to knowing the answer is 16.

But I don’t understand if we are meant to be able to do this by hand? or are we meant to put 4096 ^ 1/3 into a calculator?

I feel like I really missed something or a point since the cut was jarring

[garypettie]

Thanks for pointing this out. That is a fairly jarring cut. I’ll speak to Ben and see if he can edit this video.

I think the cut may have originally been added to explain how multiplying a number by its reciprocal always equals 1.

Put simply, the reciprocal is just a number that’s been flipped on its head.
So in this case, 1/3 x 3/1 = 3/3 = 1.
Ben uses the pie example to try and represent this concept visually.

To get to the answer of 16 you can enter 4096^(1/3) on your calculator.
Since x^1 is just x, this means that x = 16.

You can also get there by taking the cube root of 4096, which will also give you the same result.

This is because one of the index laws, which states:

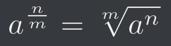
In our case, a = 4096, m = 3, and n = 1.

So we end up with a cube root and don’t have to do anything to the 4096, since it’s just being raised to the first power, which doesn’t change it.

I hope that helps clarify what’s going on but if you have any other questions please ask.

[Daniel_Thorne]

Upon reading what you said and then revisiting the video I was able to unravel Ben’s intention and hence not being as confused.

If it can be edited to be a bit clearer I think that’ll be important. I’m not sure if Ben mentioned index laws but that would’ve been cool to include in that lecture too.

But, thanks for the clarification and information!

[garypettie]

Glad I could help clear things up.

Ben doesn’t explicitly mention all of the index laws in this lecture, but the part he puts in a red box is one of them (Rule 3). The others will crop up in other videos, as we reach problems that actually require them.

For reference, there are 6 laws;

1. If you multiply terms that have the same base, then you add the indices
   

2. If you divide terms that have the same base, then you subtract the indices
   

3. If the term raised to a power is raised to another power, then you multiply the indices
   

4. If the base is raised it to the power 0, then the answer is 1
   (If the base is 0 then it’s undefined because the answer can be either 0 or 1 depending on how you look at it)
   

5. If the base is raised to a negative power, then this can be rearranged as a fraction
   

6. If the base is raised to a fractional power, then this can be rearranged as the m-th root raised to the n
   

[Daniel_Thorne]

I had/have forgotten a lot of the maths formulas and laws that I previously learnt due to the good ol’ “use it or lose it” (hence I’m refreshing with this course). However, you putting the 6 laws has jogged that part of my memory.

I’ve just got to ingrain it now! haha thanks again, and good to know to they’ll be covered with progression in the course