Hello.
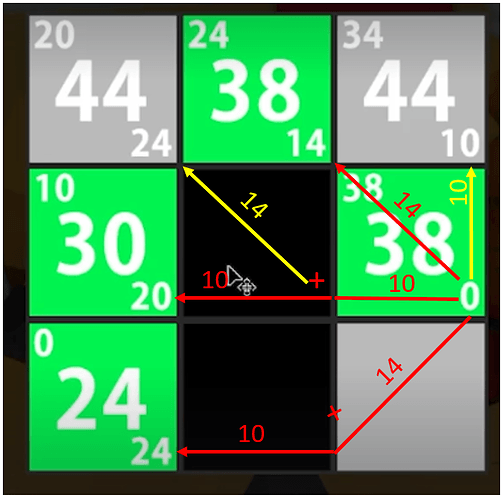
In your video, I understand what is g. an addition of each gcost from the differents tiles you use.
+10 in horizontal and vertical, +14 in diagonal.
So the first in start node is at 0, the second need 10 to move vertically so 10, the third need 14 to move in diagonal so 10+14 = 24 and the last 24 +14.
For me it’s good.
But… for the heuristic cost …
I understand heuristic solution is a solution to resolve complexes issues. It’s not optimized but do the job…
Here is the phylosophy but in reality…
I don’t understand how you pass from 24 in the first tile (it’s the same value than the start til, is there a coincidence?)
And when you go up using 10 gcost, the Hcost pass from 24 to 20… how? why ?
I don’t see the relation beetwen 24 and 20 for h and 20 to 14 then the 14 to 0.(maybe for the last one it’s the diagonal cost of 14… but it’s for me the only logical explanation…)
Thanks
François
the Heuristic cost is just a fancy way of saying “how close is this tile to the destination tile, assuming that there were no obstacles in the way”
Ideally, as the GCost increases, we want to be getting closer to the actual goal.
Imagine we’re standing at 3,3
We want to get to 1,1
Each tile around 3,3 is evaluated. The orthagonal directions have a Gcost of 10, and the diagonals have a Gcost of 14.
The HCost at this point, from 3,3 to 1,1 is two diagonal squares so 28
When we queue the squares around 3,3 we go one at a time, giving the GCost and then recalculating the H cost for each square
Imagine we first enque 4,4
The GCost from 3,3 to 4,4 is 14, the HCost from 4,4 to 1,1 is now THREE diagonal squares, or 42, meaning the FCost for 4,4 is 56
Now 4,3
The GCost from 3,3 to 4,3 is 10, and the HCost is one orthagonal square and two diagonal squares, or 38 for an FCost of 48.
From this, we can infer that 4,3 is closer to the goal than 4,4
We do this with each square around the current tile
It gets more clear when we get squares closer to the goal:
2,3 is one Diagonal and 1 Orthagonal from the goal for an HCost of 28, and a Gcost of 10, for an FCost of 38
3,2 is also one Diagonal and 1 Orthagonal from the goal, for an HCost of 28 and a GCost of 10, FCost=38
When we get to 2,2, our GCost is 14, but our HCost is also 14 (one diagonal square away), FCost = 28, so this is the closest node.
That means that 2,2 will be the next one evaluated, and we’ll check squares around this location. Once 1,1 is found in this set of valid direcitons, our search is done.
Because we used the G/H/FCost model, we only had to enqueue the neighbors of two tiles to reach our goal.
Without this GCost/HCost/FCost evaluation, assuming the same order of operations, we would have wound up enqueing the neighbors of at least 9 squares to read our destination, as we wouldn’t have a reliable method of determining if we were closer or further from our goal.
In a grid with no obstacles, the number of evaluations required to get to the destination is n + 1 where n is the number of tiles distant from the source to the destination. This increases as we add obstacles to the scene.
Without the added heuristics, the total number of evaluations can be significantly higher… as much as n * n evaluations.
Hello Brian !
Thanks for this very complet and full reply 
I’ve opened my mail this morning but seeing the lenght I’ve decided to read it this evening.
So before I knew Eurythmics with Anny lenox now I know Heuristic with Brian Trotter 
It completly clear now.
In fact Heuristic way is always the most direct way from a node to final destination.
I’ven’t understood in the Code Monkey overviewing that an euristic solution doesn’t take care about black tile.
So the addition of the H cost and the G cost allow to reach the lowest neighbourg tile in F cost around the actual tile.
It’s very nice and smart.
Thanks a lot to have spent time to clarify this point.
Have a nice day.
Take care.
François
I’m glad I could help!
This topic was automatically closed 24 hours after the last reply. New replies are no longer allowed.