Feedback on understanding of normalized vectors

[MyCody]

I’m trying to understand why we normalized the vector before moving the map. I think I understand, and I’m looking for feedback on my understanding. Here’s the code from the lecture:

  Vector2 mapPos{0.0, 0.0};
  while (!WindowShouldClose())
  {
    BeginDrawing();
    ClearBackground(WHITE);

    Vector2 direction{};
    if (IsKeyDown(KEY_A)) direction.x -= 1.0;
    if (IsKeyDown(KEY_D)) direction.x += 1.0;
    if (IsKeyDown(KEY_W)) direction.y -= 1.0;
    if (IsKeyDown(KEY_S)) direction.y += 1.0;
    if (Vector2Length(direction) != 0.0)
    {
      // bellow is the line in question
      mapPos = Vector2Subtract(mapPos, Vector2Normalize(direction));
    }

    DrawTextureEx(map, mapPos, 0.0, 4.0, WHITE);
    //...
  }

every tick direction is reset and updated if a key is pressed. The direction updates the mapPosition. The map is drawn with DrawTextureEx() and the second param is the location, mapPos, to draw the map.

I tried it without Vector2Normalize()
mapPos = Vector2Subtract(mapPos, direction); instead of
mapPos = Vector2Subtract(mapPos, Vector2Normalize(direction)); and it moves the map just fine. My understanding is a vector is a distance and direction, whereas a normalized vector is just a direction.

Here’s a screen shot of my debugger after hitting the S and D keys simultaneously (I’ve pressed a few keys and moved the map to (-5,-3) before doing this):

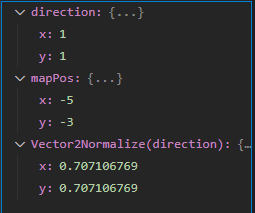
So if I use mapPos = Vector2Subtract(mapPos, direction); the map would move to (-6,-4).
If I use mapPos = Vector2Subtract(mapPos, Vector2Normalize(direction)); the map would move to (-5.7,-3.7). It’s a subtle difference. I’ve played games where the player can move across the world faster while pressing both W and D together than just pressing the W key, I’m assuming because that dev didn’t use a normalized vector.

[Tuomo_T]

That’s correct! We’re wanting the player to move at a certain speed regardless of the direction they’re moving. This works fine if they’re moving in one of the cardinal directions (up, down, left, right) which keeps the vector at the appropriate length. Since the length of the direction vector will always be 1 in our case.

But when moving diagonally, the length of the direction vector becomes the square-root of 2. So we have to normalize the vector by dividing it’s x and y coordinates by its length. Which is what the normalize function is doing.