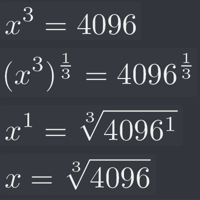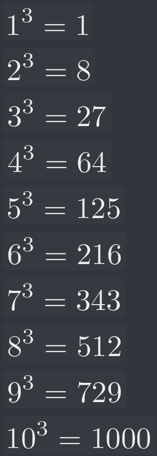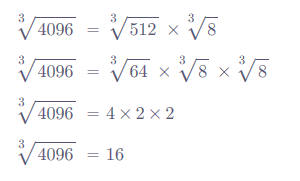Did I miss something in the solution?

[Traziel]

I’ve read the previous posts and Gary’s responses, and I still feel like we’ve glossed over the actual “solving it” piece.

The video details each minor interim step to breaking the problem down to 4096^(1/3) in order to get the solution. Then, at 5:51, after the odd spliced in explanation, Ben says “and how do we figure out what 4096 to a third is? Well, you can do that by popping it into your calculator…” Gary’s reply also says “put it into your calculator.”

There’s this build-up of rules and steps, and the final anticlimactic step is “use your calculator.” I obviously could have put “4096^(1/3)” in my calculator (or otherwise googled the cube root of 4096) and saved 7 minutes of video, but I want to know how to do it myself. This is like going on a quest to learn the secret of human flight, and then the final step is “get in an airplane.”

[garypettie]

Hi Traziel,
This is one of those things in math where using a calculator really is the easiest method if you want an exact answer.

If you want to do it by hand there is a handy little trick to solving cube roots.

Now, this method is specific to cube roots and there are other approaches you can take (like the division method).
For the most part, all of these take some amount of brute force or memorizing a subset of known cubes. So with calculators available it’s always going to be easier to use one for these types of calculations.

Here’s the general process using the example from the lecture;

1. Clean up our equation to make it easier to work with…
   
   Now we’re in a form that has isolated x and also cleared things up on the right.
   This is pretty much where we left things in the lecture.

2. For this method you need to already know the first 10 cube roots.
   If you haven’t memorised them (because why would you) you can quickly work them out on paper.
   

3. Now when we look at the number we’re trying to solve, break away the last 3 digits.
   So you’re now working with 4 and 096.

4. Find the answer from our table that is lower than or equal to the first part of our number.
   Then take the base of that number to be our answer. For us, this is going to be 1
   

5. With the last 3 digits, we’re going to compare the final digit with the final digit from out list of cubes.
   In our case, the last digit is 6 and this matches 6^3, so the last digit of our answer is 6.
   

6. Combine our answers to get 16.

[jbwb]

The easiest way to do complicated cube roots is to break it down into cube roots you can solve.

Here’s how I solved cube root of 4096:

This method only applies to numbers that actually have a whole number as a cube root. If you run into a number that doesn’t have an easy cube root, you just have to gauge which whole numbers the answer likely lies between and then estimate using fractions.

[OuterGazer]

I think there is a simpler way of resolving cube roots (or roots in general) that is similar to the solutions provided but I think it’s simpler. It’s called “Factorization”. You take the number you want to “root” and systematically divide it by the smallest integer below 10 that we can each time where the reminder is 0 until we reach 1. Let’s see it in practice:

4096 | 2 (on the next line we put the number that comes out of dividing 4096 by 2)
2048 | 2 (still even, so we can divide by 2 again)
1024 | 2 (still even)
512 | 2 (still even)
256 | 2
128 | 2
64 | 2
32 | 2
16 | 2
8 | 2
4 | 2
2 | 2
1 (and we stop once we get to 1)

To go back to 4096 we need to multiply all those 2s we have there. This means that 4096 = 2^12. That is that our x = CubeRoot(4096) can be written as:
x = CubeRoot(2^12)

The indexes above, following the (a^b)^c rule we learned, could be written as follows:
x = (2^12)^1/3 --> or x = 2^(12/3) which is 2^4…
or 2 * 2 * 2 * 2 which equals to 16, out answer.

[flashjaysan]

@Traziel I think you missed the whole point of that lecture.
The purpose of it was to explain how to solve an equation that is in the form :
x times x times x = something
The solution is :
x = cube root of (something)
You don’t have to calculate the true real value because it may be an approximation, not a precise value.
In the lecture example, 16 cubed is 4096 and so the cube root of 4096 is 16 (a whole number). But what if you wanted to calculate the cube root of, let’s say, 777? You’d get something close to 9.193
And in algebra, you cannot use approximations as solution so the real notation that you cannot simplify is just cube root of (777)
So, to recap, the real purpose of the lecture was to explain how to express x when we only know its cube. The answer is just cube root of its cube. The actual value is irrelevant.