Comparing the complete functions of N^2 vs (n log n)

Unreal Courses Talk
,
#1

To calculate total processing time, I wanted to graph the entire process, not just the sorting or just the one check. So I included the entire check process. So, when I graph

(n^2 - n )/2 vs (n log n)+n, n=2 to 17

on Wolframalpha, I get the following graph:

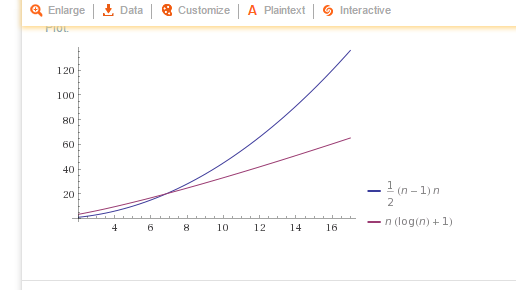
I see there is a point in which each function intersects. As this intersection of sets occurs in the positive quadrant of the graph, and (for our purposes) rather far into what our range of letters would be, I am inclined to say that we should provide both sets of algorithms for the code to use.

The intersection lies at about 7, so I would argue the following provides maximum efficiency:

if (word.length <=7) {(n^2-n)/2)};
else {(n log n) + n;

I am a high school math teacher, (though I don’t hold a math degree, rather a music degree.) so I understand the math part of it, mostly, but not all the coding/computer processing part of it, so I admit I may be missing something big here. Also, I understand that the difference in speed would be negligible for a program this size on modern machines. But of course we have to start thinking efficiency now, so later on our large programs work efficiently.

Really interested in what the instructors, @ben and @sampattuzzi, have to say about this.

EDIT:
Also, I wrote this before I saw the challenge to vote for the fastest. So… I guess this is my vote.

EDIT 2:
AAAAAAAND Of course I’m wrong. But still. I want to hear thoughts on this, to see if I’m “thinking like a programmer”

#2

When talking about big-O we generally want to see which is the slowest/fastest growing. Even if there is an early advantage, this is likely highly affected by other factors in programming such as caching, disk accessed, efficiency of the instructions used. However, big-O excluse all these factors and answers the question “Will it scale?”.

In our given example it’s a bit of a toy because we don’t ratchet the complexity up (in fact the limit is the size of the alphabet). But in many applications, this is important, e.g. how many vertexes can we paint in one frame?

Privacy & Terms