If you’re reading this, there probably aren’t very many posts yet. But don’t worry, you can be the first! Either create a new post or just reply to this one to say ‘hi’.
The Unity package for the updated Windmill isn’t attached in the resource for this lesson.
edit and it’s there now!
Thanks for pointing this out.
Hey so I thought it would be cool to have a random ‘WindIsBlowing’ bit of functionality where the windmill randomly stops for a time.
I feel pretty good about the logic but apparently Random.Range is a heavy load in update as the rotation starts chunking like crazy when I added that function (twice)… any suggestions for something else? Here is what I was thinking ( basically every frame check to see if the wind is still blowing, if its not I was going to slow the rotations to a stop and wait a random number of frames) – see comment near the bottom of if statement.
if (windIsBlowing)
{
//xDegreesPerFrame = Time.DeltaTime, 60, xRotationsPerMinute, 360
//// Debug.Log("Time : " + (60 - Time.deltaTime));
//Debug.Log("Degrees Per Minute : " + (360 * zRotationsPerMinute));
//Debug.Log("Degrees Per Second: " + (360 * zRotationsPerMinute) / 60);
////Debug.Log... got it!
float xDegreesPerFrame = ((360 * xRotationsPerMinute) / 60) * Time.deltaTime;
transform.RotateAround(transform.position, transform.right, xDegreesPerFrame);
float yDegreesPerFrame = ((360 * yRotationsPerMinute) / 60) * Time.deltaTime;
transform.RotateAround(transform.position, transform.up, yDegreesPerFrame);
float zDegreesPerFrame = ((360 * zRotationsPerMinute) / 60) * Time.deltaTime;
transform.RotateAround(transform.position, transform.forward, zDegreesPerFrame);
//Give a 1 in 20 chance of not spinning ( wind stopped blowing )
// windIsBlowing = Random.Range(0, 20) < 18;
// if (!windIsBlowing) windStoppedFrames = Random.Range(5, 10); //Set the amount of frames to keep the wind stopped
Debug.Log(windIsBlowing);
Debug.Log(windStoppedFrames);
}AND … how do you get that glow in the windows of the windmill? I want that glow and I have a forge I would love to be able to add glowing embers too…?
As a bad programmer with poor math skills describing how to do this via code comments didn’t help me at all. I was left totally confused! Even after watching the solution I have no idea what happened and I still don’t know why we multiply by “to the minus 1”!
What I think would’ve helped is to demonstrate this visually with scribbles like Kahn Academy. It would give me a visual model what I’m actually doing and allow me to recognise it again if I were to come across it elsewhere.
I’m pretty decent at maths and this video’s comments threw me off as well.
I think I’m not familiar enough with this way of calculating.
I agree that functions should be well thought out rather than the try-until-it-works approach,
but in this case I felt the solution was overly complicated.
@tvance929 I like your solution, easy to read: ((360 * xRotationsPerMinute) / 60) * Time.deltaTime
Varying wind speed is a good idea. Suggestion: pick a random target speed every 5 or 10 seconds, then linearly interpolate toward that speed using Mathf.lerp(). This way you get a smoothly animated change in speed, you can even stop it sometimes.
Thanks…unfortunately I had to use the ‘try-until-it-works approach’ because I couldn’t quite grasp Ben’s method either.
And thanks a ton @Martin for the wind suggestion… i’ll get back and try that soon and let you know how it works for me!
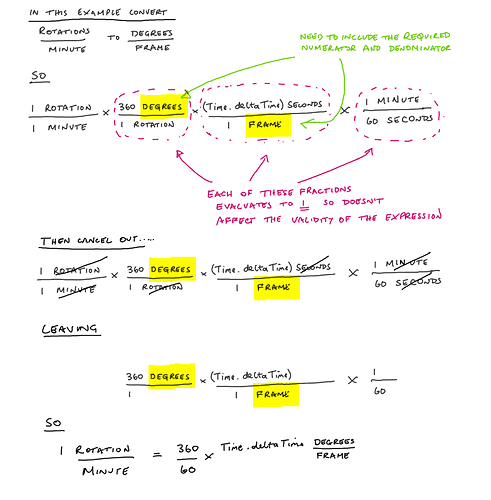
it’s an interesting approach. Here’s the way that I would normally go about solving a problem like this. Might be useful to anyone who is getting confused by the dimensional analysis idea.
Basically, it boils down to doing it one step at a time until you are using all the variables you have at hand.
Aim is to express degrees per frame in terms of seconds per frame (which is Time.deltaTime) and rotations per minute.
degreesPerFrame = degreesPerSecond * secondsPerFrame
= degreesPerSecond * Time.deltaTime
= (degreesPerMinute / 60) * Time.deltaTime
= (rotationsPerMinute * 360 / 60 ) * Time.deltaTime
= rotationsPerMinute * 6 * Time.deltaTime
I’m sorry but this is possibly the worst explanation of dimensional analysis I have ever seen. It would be better to just read Anya’s comment than watch this video.
For anyone struggling with the exponent notation, I thought I’d chime in with what’s going on. This builds on Anya’s excellent response (although for clarity I wouldn’t factor out the 360 / 60 in her example;) )
So, without further ado lets get ready for a quick-fire maths lesson - don’t worry, it’s not too painful! …
Note: I’ve put Math terms in codeblock so you know what to Google.
Note 2: I’ve tried to inject some humor into the post, maths can be really boring and/or really intimidating. Don’t let it scare you. Once you get the hang of it it’s the most useful skills you’ll ever learn.
Hopefully, you’ve all seen positive exponents before. Things like x^2 (x squared), x^3 (x-cubed) etc.
(exponent is just a fancy word for ‘powers of’ - look at us, smarter already!).
This is just a way of saying “times x by itself that many times”, So x^2 = 2 * 2, x^3 = 2 * 2 * 2, etc.
When it comes to negative exponents, you need to understand the basic Index Laws and something call the reciprocal of a number.
Imagine the number 9… Well, don’t imagine it, it’s right there…
Take that number 9 and think of it as a fraction of 1. You get 9/1 right?
Well the reciprocal is just that number on it’s head. Which is 1/9.
The great thing about this fact is that any number multiplied by it’s reciprocal equals 1.
9/1 * 1/9 = 1
Making sense so far? I hope so!
The next thing you should remember is that division is basically the opposite of dividing.
So, 9/1 * 1/9 = 1, as does 9 / 9 = 1.
See where we’re going yet? If not, all will be revealed soon!
Now, we know that multiplying a number by itself raises the exponent, so it would make sense if dividing the number by itself lowered it, right?
Now, if you’ve googled your index laws (or just happen to remember them) you’ll know that anything raised to the power of 1 stays the same, so 9^1 = 9,
So what happens when we combine everything that I’ve just rambled on about?
You should see that 1/9^1 is the same as 9^(-1).
More generally, you’ll see that 1/a^(n) = a^(-n) - (aaagh, algebra, quick, hide!)
Well, lets try and apply that back to the units (distance and time) with everything we’ve just covered.
m/s = m / s^1 = m s^(-1)
Make sense?
Regardless of the form they are read as "metres per second"
So meters per second squared = m s^(-2), and so on.
It’s worth mentioning that when you read maths/physics formulas, you’re likely to see these negative exponents a lot because they are generally easier to read and understand than the fractional notation.
In isolation the second option may seem easier, but as the formulas become more complex the whole thing can get a bit confusing.
So there you have it. You made it to the end. Go grab a glass of your favourite adult beverage and breathe.
Hopefully that wasn’t too painful and hopefully I made things a bit clearer for anyone struggling.
I’m happy to help anyone who is struggling with their maths, so drop me a message if you want to chat. I’d also recommend Khan Academy, which is an excellent (and free) resource that covers everything from basic counting to calculus, and beyond.
P.S. If you found this explanation helpful and would like me to write something up on dimensional analysis, please let me know. I think Anya already gave a pretty good answer to the problem, so just decided to focus on the whole negative exponent thing.
Makes so much more sense! Thank you for sharing.
I’ve an A-Level in Maths (admittedly rather a long time ago) but I was totally thrown by the video explanation.
Same here. I’m ok with Maths, but struggled to understand the working as described… I went this way (very similar to Anya)
We have… R Rotations per M minute. ie. R/M
Lets convert to degrees per second… 1 rotation® = 360 degrees, 1 minute = 60 seconds. So…
R360/60
= R6
So R. Rotations per minute = 6R Degrees per second.
Now we need to make it per frame. We have done this plenty of times before… 6 * R * Time.DeltaTime
Yeah, not getting the convoluted formula speak in these last two videos either; as bad as I am at math, I’ve done basic trig to animate wheel of fortune style dragging games, so I’m no stranger to this kind of animation. But this weird raising everything to the power of -1 just isn’t doing it for me, sorry. Good old fashioned enforcement of operation order using parentheses and local variables work just fine, and I couldn’t care less about anyone else who has to read my math.
((zRotationsPerMinute * 360) / 60) * Time.deltaTime, just from working it out in my head with common sense. AKA degrees per minute / 60 seconds = degrees per second, multiplied by Time.deltaTime.

A fairly minor point but it struck me that just dropping the numbers 60 and 360 in the calculation wasn’t too clear and this seemed to be a good time to iuse const. So I defined two consts:
const float secondsPerMinute = 60f;
const float degreesPerRotation = 360f;
These could then be used in the calculation.
float xDegreesPerFrame = (Time.deltaTime / secondsPerMinute) * degreesPerRotation * xRotationsPerMinute;
This was really poorly explained.
The simple example in Wikipedia does a much better job
So in this example …
Yes, took the same route