About 'Breadth First Search Algorithm'!

Unity Courses Talk
, ,
#1

In this video (objectives)…

  1. Look at the Wikipedia article on BFS
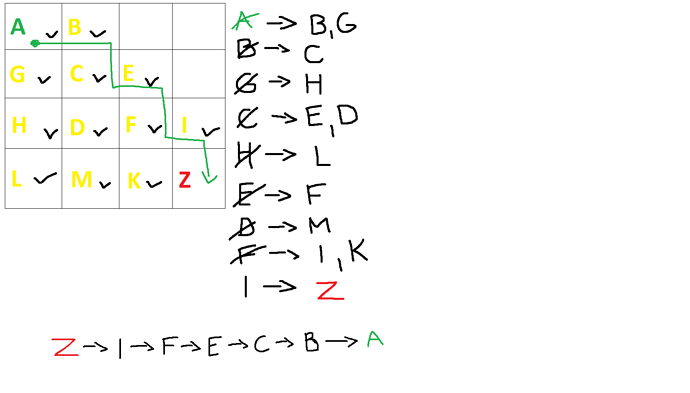
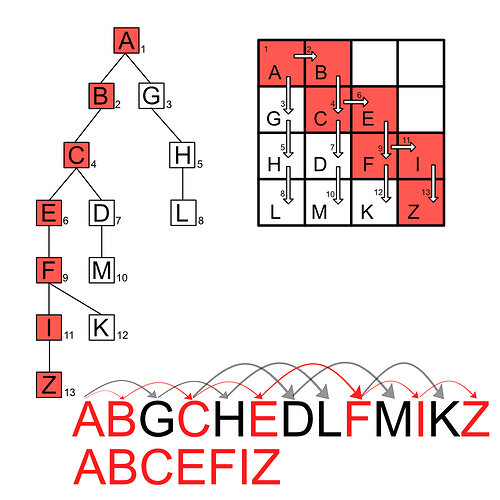
  2. Demonstrate simpler pseudocode for BFS
  3. Walk through BFS step-by-step.

After watching (learning outcomes)…

Manually perform Breadth First Search, and find the shortest path.

(Unique Video Reference: 13_RR_CU2)

We would love to know…

  • What you found good about this lecture?
  • What we could do better?

Remember that you can reply to this topic, or create a new topic. The easiest way to create a new topic is to follow the link in Resources. That way the topic will…

  • Be in the correct forum (for the course).
  • Be in the right sub-forum (for the section)
  • Have the correct lecture tag.

Enjoy your stay in our thriving community!

#2

for the challenge wouldn’t the order be

abgchedLfmikz

ab
gce
hdfi
lmkz

a-b-g-c-h-e-d-l-f-m-i-k-z
(point) = (what you “see” from point) (The searched list)
= a (a)
a = bg (abg)
b = c (abgc)
g= h (abgch)
c = ed (abgched)
h = l (abgchedl)
e = f (abgchedlf)
d = m (abgchedlfm)
l = nothing (abgchedlfm)
f = jk (abgchedlfmjk)
I = z (abgchedlfmjkz)

(or if you need a tree diagram)
the | indicates a “new” branch, the letter in the “brach” indicates the branches parent

a
(a)bg
(b) c | (g) h
© ed | (h) L
(e) f | (d) m | (L) null
(f) IK | (m) null
(I) z | k
(z) null

1 Like
#3

So I got a result of:

A B C E F I Z

‘un-pauses video and hopes for the best’

#4

Que: ABGCHEDLFMIKZ

path: ABCEFIZ

so same as everybody else

#5

A-B-G-C-H-E-D-L-F-M-I-K-Z
I imagined the fields like ticking watches. One starts the others according to the clock’s directions.
Path

A-B-C-E-F-I-Z - firs shortest path

#6

I got the path A -> B -> C -> E -> F -> I -> Z as well.

Explanation:
Start -> Add A to Queue -> Current Queue = {A}
Round 1 -> de-queue A and explore -> Found B and G in that order because of up/right/down/left precedence, add to queue -> Current Queue = {B, G}
Round 2 -> de-queue B, explore -> Found C, add to queue -> Current Queue = {G, C}
Round 3 -> de-queue G, explore -> Found H (C already queued), add to queue -> Current Queue = {C, H}
Round 4 -> de-queue C, explore -> Found E, D, add to queue -> Current Queue = {H, E, D}
Round 5 -> de-queue H, explore -> Found L, add to queue -> Current Queue = {E, D, L}
Round 6 -> de-queue E, explore -> Found F, add to queue -> Current Queue = {D, L, F}
Round 7 -> de-queue D, explore -> Found M, add to queue -> Current Queue = {L, F, M}
Round 8 -> de-queue L, explore -> Found nothing new -> Current Queue = {F, M}
Round 9 -> de-queue F, explore -> Found I, K , add to queue -> Current Queue = {M, I, K}
Round 10 -> de-queue M, explore -> Found nothing new -> Current Queue = {I, K}
Round 11 -> de-queue I, explore -> Found Z (target)

tracing back our steps, we see Z was found from I, which was found from F, which was found from E, which was found from C, which was found from B, which was found from A

so the path is A -> B -> C -> E -> F -> I -> Z

#7

Queue order would be - ABGCHEDLFMIKZ

So, tracing back it would go - Z-I-F-E-C-B-A

Which would make this the shortest path - A->B->C->E->F->I->Z

Which, nicely seems to match what others put…

#8

I got:
A -> B -> C -> E -> F -> I -> Z

#9

I used paint to write and illustrate the shortest path:
Using UP, RIGHT,DOWN,LEFT we reached Z from I, I from F, F from E, E from C, C from B, B from A.
So our path will be: A B C E F I Z:

AtoZ
AtoZ.png1711×977 20.5 KB

1 Like
#10

My solution :slight_smile:
Queue order: ABGCHEDLFMIKZ
The shortest path: ABCEFIZ

BFS_system_2
BFS_system_2.jpeg1000×1000 243 KB

#11

My order was
A-B-G-C-H-E-D-L-F-M-I-K-Z
Shortest path was
A-B-C-E-F-I-Z

#12

order
SO shortest path is BDG

Privacy & Terms