Hello,
I really do not get how th integers are stored. The first 4-bytes (from 0x00 to 0x03) is said to store the integer 8. Great, so the the first value in the table is the integer… strange but ok… so the second 4-bytes is 20… no it is 32. Why?
thanks,
Gatien
Because it’s displayed in hexadecimal which is base 16.
We, humans, count in base 10 so we have 10 symbols to display numbers 0 to 9.
Once we run out of symbols we reset back to 0 and increment the next digit
08
09
10
From right to left they are increasing powers of 10 starting at 0.
1 0 1
10^2 10^1 10^0
100 10 1 = 101
Now to bring it back to hexadecimal. Instead of 10 symbols we have 16
0-9, A-F.
So instead of each being worth a power of 10 they are worth a power of 16
1 0 1
16^2 16^1 16^0
256 16 1 = 257
Hi,
Just to jump onto Gatien question, is it correct to say that the memory location it is located in (0x10 - 0x13) makes no difference, i.e. it could be in 0x04-0x07, it is the fact that it is 20 (two lots of 16) means it is 32?
Thank you
Dave
Sorry I didn’t notice you replied. But yes, where it is doesn’t matter.
I want to help out anyone that comes across this because it is very confusing the way it is described in the video, and while the answers here have merit, it can be a bit hard to piece it together.
As mentioned, hexadecimal is base 16. To better understand this, lets look at how we get 20 with base 10, which is what we are accustomed to.
In base 10, we multiply n by the corresponding position’s power of 10. The position (what you will raise 10 to) starts with a 0 index and increases from the right to the left, so the 0 in 20, is position 0, therefore we get that value from:
0 * 10^ 0, which equals 0.
For the 2 in 20, the position is 1, so we get the value from:
2 * 10^1 (10^1 = 10 * 2) = 20.
So now lets apply that same logic to base 16.
0 * 16^0 = 0
2 * 16^1 = 32
that is how we get 32. as far as the other 00 00 00 in the next three cells, that is simply because an integer requires 32 bits, which is 4 bytes (each blue square is a byte), but don’t let those numbers confuse you in the calculation of 32, that is only done by the 2 and the 0.
Wow thank you this table is litteraly all I needed to understand
No worries!
I didn’t get it but understand it now. I think Big and Little Endian confusing. Little Endian is the normal way we write numbers I think.
That would be big endian.
Given the hexadecimal number
0A0B0C0D
Little Endian:
0D
0C
0B
0A
Big Endian:
0A
0B
0C
0D
Big endian puts the most significant byte first. Whereas little endian puts the least siginificant byte first.
I’m starting to grasp the 16^X power system, but I don’t understand how we got 2 to determine we were multiplying 16 by 2 with a 20 being there.
From what I understood in the lecture a 20 is being stored in the 4 bytes? Is that right?
From what I understand with the first one where an 8 is being stored so it is in the 16^0 so:
16^0 = 1
8x1 = 8
If its in the 16^1 it should be 20 x 16 no? So it would be 320.
Why is 20 suddenly 2? while 8 remains untouched.
I do not grasp where the 2 comes from.
EDIT:
I got some clarification from a friend it appears to be bytes not bits everything is stored in which explains the fact the bool is only 1 block on the chart.
However, I am still confused how to get 32.
20 in base 16 is 32 in decimal
2 0
16^1 16^0
Anything to the power of 0 is one, so the right hand most column is worth 1.
16 to the power of 1 is 16.
So putting that together, we have 2 lots of 16 and 0 of 1.
2 * 16 = 32.
We, humans, count in base 10 so we have 10 symbols to display numbers 0 to 9.
We may count in other bases as well such as 12 for foot/inches so it really depends on the context though. eg 2 feet is 24 inches not 20 that the 10 base would give.
I think its something that many don’t think about and may calculate on other bases without even realizing. However, in programming it is an entirely other thing to take into consideration.
Oh i see. That does clarify it thank you.
Yeah, I meant read rather than count.
I did a bit of searching online to figure this out and just wanted to add my own explanation.
In our every day number system, numbers 0 - 9 are a set of 10 numbers. Once we reach the end of that set, we start counting the second set which is 10 - 19, also a set of 10 numbers, the third set being 20 - 29 and so on.
Additionally, the components of any number you come up with falls under a certain digit:
For example 335 is 3 in the hundreds category, 3 in the tens category, and 5 in the ones category
Meaning, we have 3 one hundreds, 3 tens, and 5 ones = 3x100 + 3x10 + 5x1 = 335
Another way of writing the digits is:
Ones = 10^0 = 1
Tens = 10^1 = 10
Hundreds = 10^2 = 100
etc…
Using the above, you could technically write 335 in this way: 3x(10^2) + 3x(10^1) + 5(10^0).
In hexadecimal its done differently.
The sets here go from 0 to F, with the letter F representing 15. Each set therefore has 16 numbers. The next set goes from 10 to 1F, (I like to think of it as “one-zero to one-F”). And the next is 20-2F etc.
Since the sets are different, the digits are as well. So intsead of 100s, 10s, and 1s, we have 1s, 16s, 256s etc.
Ones = 16^0 = 1
Sixteens = 16^1 = 16
Two Hundred and Fifty Sixs = 16^2 = 256
Compare this with the above 1s 10s 100s.
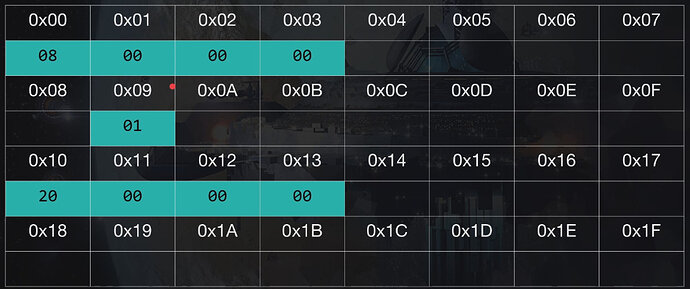
Now, in the example in the course we have number “8” and number “20”.
Well, 08 is basically zero 16s and 8 ones which is why we get 8. Mathematically we write:
Now with number 20 we have two 16s, and zero 1s:
Now you can tell all your friends that 20 = 32.
Great explanation 
Ok so I’m getting how the hexadecimal system works but in the example there is a boolean for some reason. Why? Why is the boolean stored where it is? How can you tell its a bool?
To be another example
There is no reason. It could go anywhere, it’s an example.
You can’t. Could be a char, or any other 1 byte type.