2018-09-13 (12:20 AM)

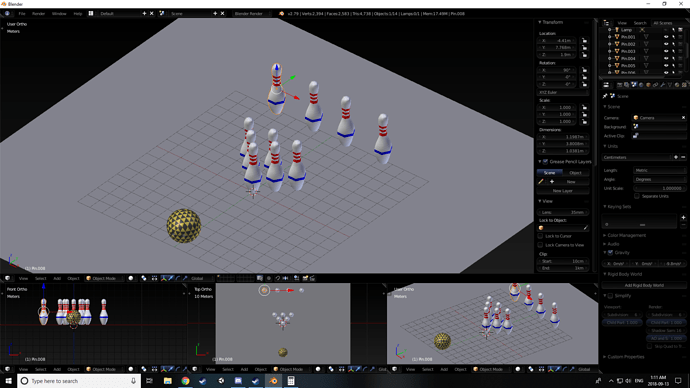
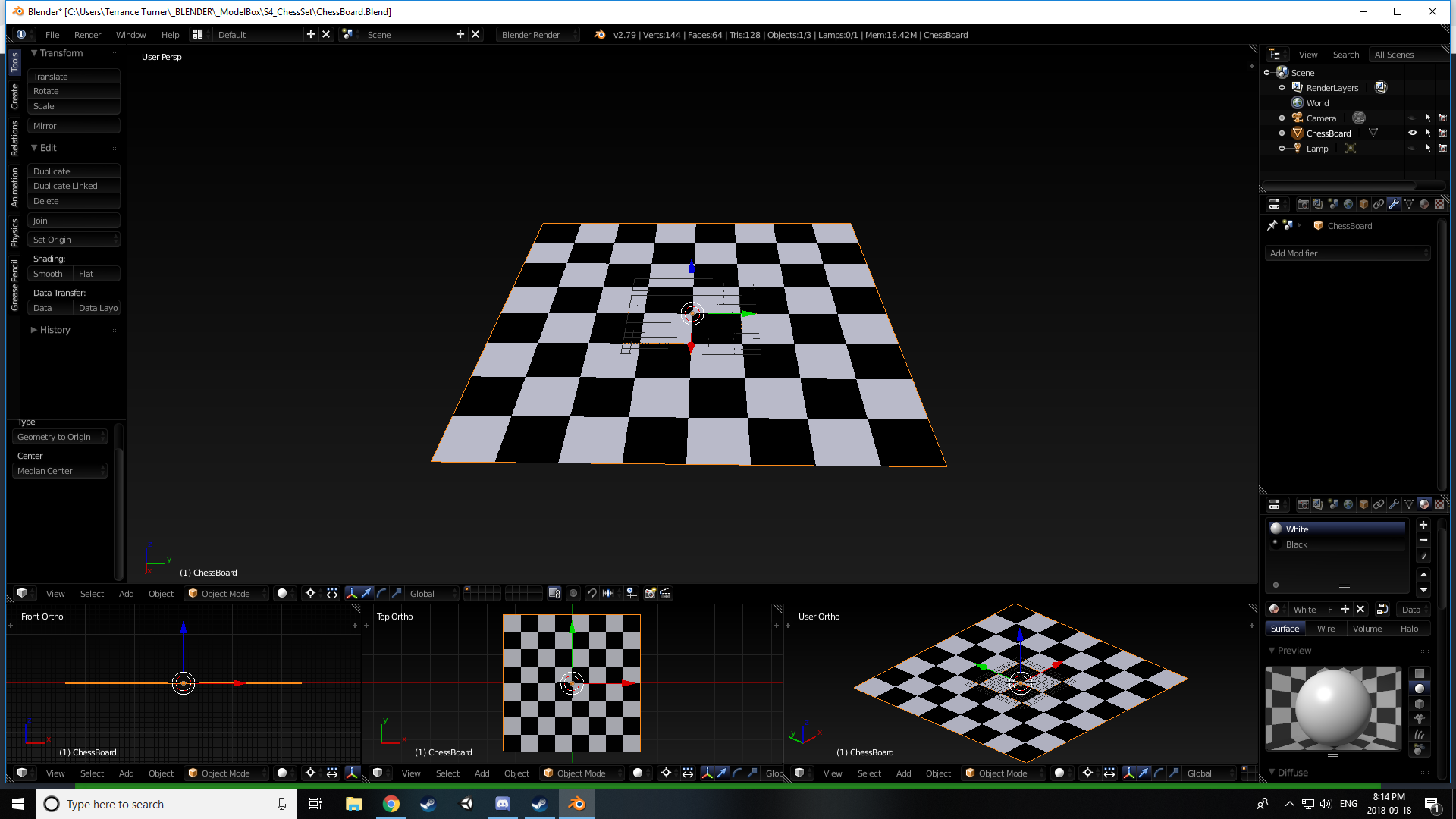
I’ve got a Lovely bunch of bowling pins


There they are, all standing in a rowwwww

Edit#1 (12:30 AM)
now they’re in their general positions, now i just gatta math out what the actual spacing is, and how to use it in my blender units. Cuz they’re 12 inches apart but my models are in cm sooooo
12inches x 2.45 = 30.48cm
now using Pythagorean theorem i should be able to figure out how far along the X and Y axis i need to move each pin
Edit#2 (12:42 AM)
so i know that from the center of the first pin to the center of the back, right pin is 36inches
i Also know that they are placed in an equilateral Triangle. So that means the back row is also 36 inches
so if i was to cut the placement in half, i’ll have a right angle triangle with the sides of 18 inches (half of 36), 36 inches (the hypotenuse) and X. so
18(squared) + X(Squared) = 36(Squared)
324 +X(Squared) = 1296
subtract 324 from both sides of equation to isolate X
X(Squared) = 972
X = 31.17 inches
so the Coordinates i have to move my furthest pin is (31.71, 18, Z)
BUT WAIT, i’m in cm and these coordinates are in inches.
31.71 x 2.45 = 77.68cm
18 x 2.45 = 44.1cm
which leaves my new Coordinates as follows: (77.68cm, 44.1cm, 1.9cm)
And after much fiddling around i forgot the pins and ball were made upscale by 10x
sooooooooo guess we’re working in meters.
so new coordinates for the furthest pin is (7.768m, 4.41m, 1.9m [that’s just so they sit atop the plane we made)
and they are each spaced out by 3.048m
so the back row Coordinates will be
#7 (7.768, 4.41, 1.9)
#8 (7.768, 1.362, 1.9)
#9 (7.768, -1.362, 1.9)
#10 (7.768, -4.41, 1.9)
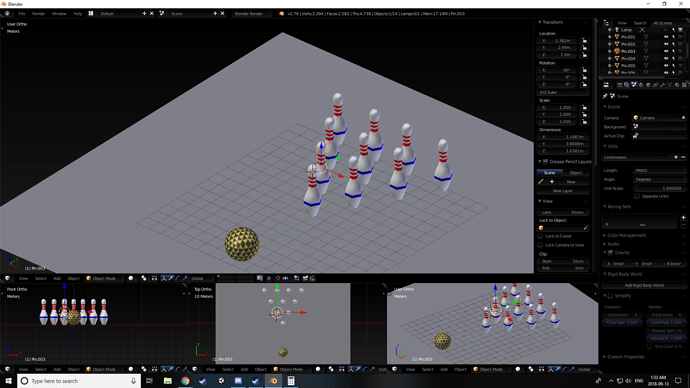
and after putting that in mine, i see that i have my axis backwards but still got the same result.
now to figure out the others
okay so their all 3.048 from eachother, so if i was to match the coords of one of the third row pins with the corner pin, i should be able to move it half of the spacing between pins (1.542) along the x axis then along the y axis cuz they form equilateral triangle right?
well i tried it and it failed XD
alright well back to Pythagoras’ theorem
A = half the distance between pins, so 1.542
B = ?
C = full distance between pins sooo 3.048
I’m cutting the equilateral in half
A(Squared) + B(Squared) = C(Squared)
1.542(Squared + B(Squared) = 3.048(Squared)
2.322 + B(Squared) = 9.29
B(Squared) = 6.968
B = 2.639
I’mma start rounding to the nearest 100th from now on
#4 (-2.886, 5.129, 1.9)
#5 (0 , 5.129, 1.9)
#6 (2.886, 5.129, 1.9)
#2 (-1.362, 2.49, 1.9)
#3 (1.362, 2.49, 1.9)
#1 (0, 0, 1.9)
Well there is all my work to get to this scene
Jeeze i gatta look at some other folks and see how they did on this, cuz damn i think i went a real hard way to get all the maths right. 
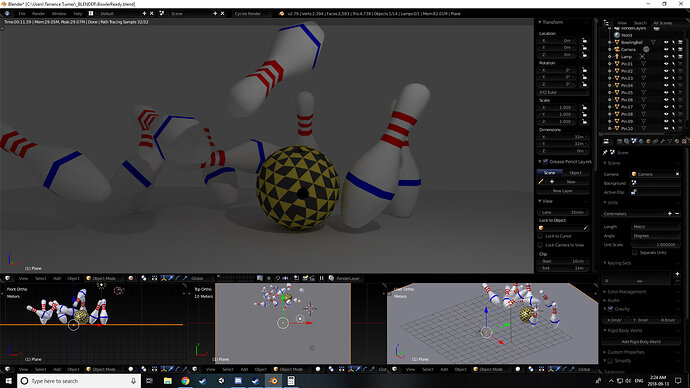
Oh by all that is good and holy in this world. Just watched @Michael_Bridges solution to creating the extra pins and setting them up… QnQ owwwwww my brain. Why did i do that to myself… Oh jeeeeeze. I’m glad and all that i completed the challenge and after watching the vidja i know how to do it better and more efficient in the future.

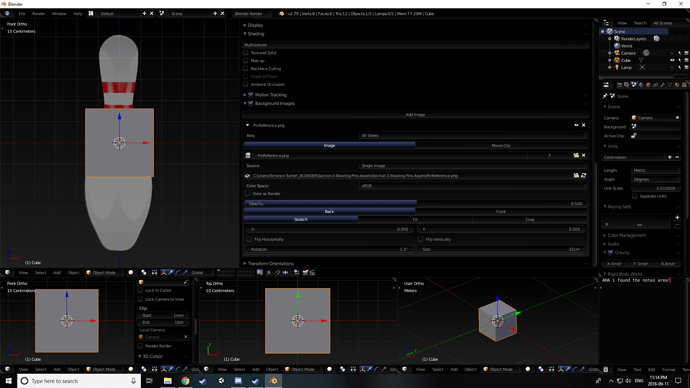
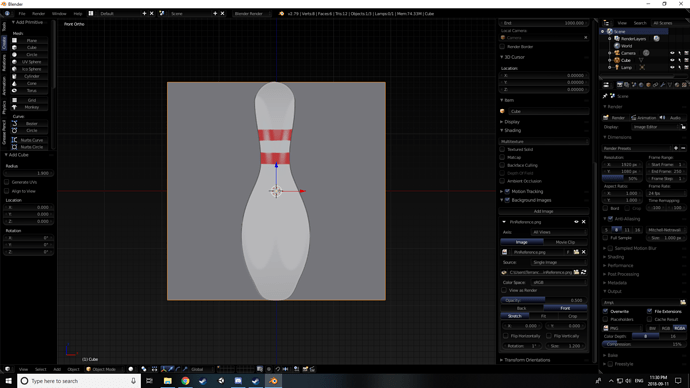
 . As a note of import: adjust the radius of a created cube and all other cubes created after it have the same adjustment. Probably a good thing but it caused me to panic when i couldn’t delete it and work from step 1 again to try and figure out why we were adjusting it.
. As a note of import: adjust the radius of a created cube and all other cubes created after it have the same adjustment. Probably a good thing but it caused me to panic when i couldn’t delete it and work from step 1 again to try and figure out why we were adjusting it.
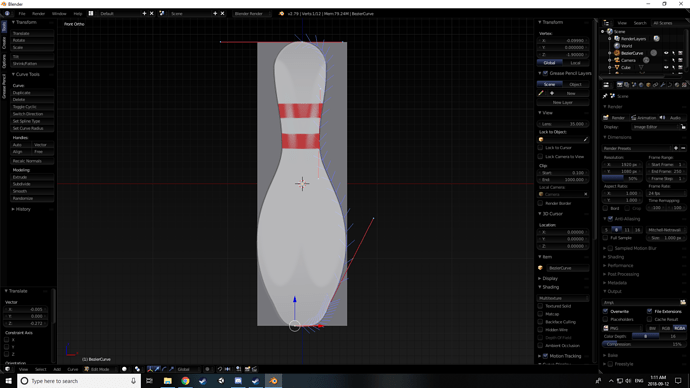

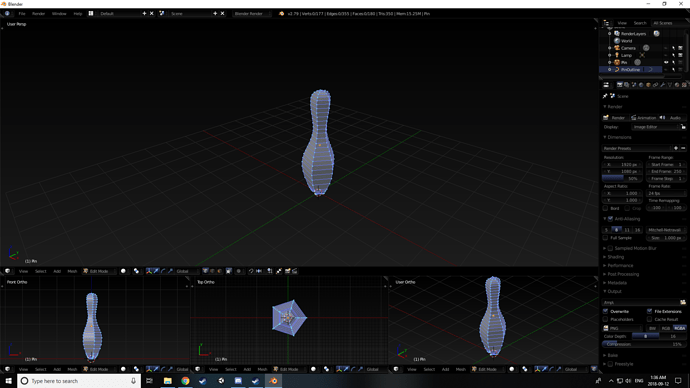
 jk jk
jk jk




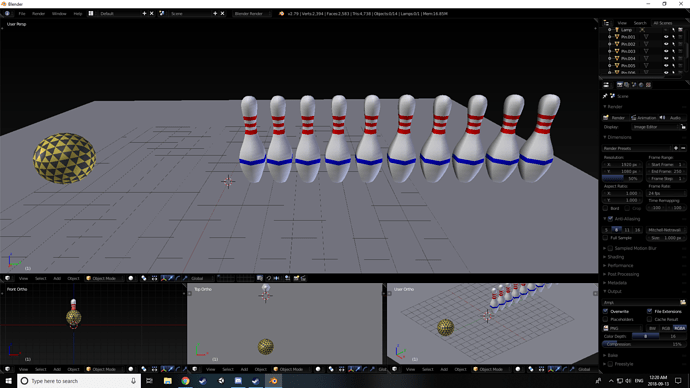
 I’ve got a Lovely bunch of bowling pins
I’ve got a Lovely bunch of bowling pins