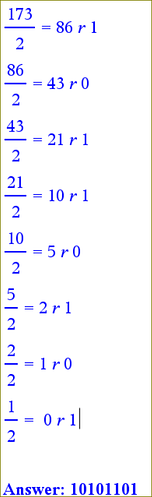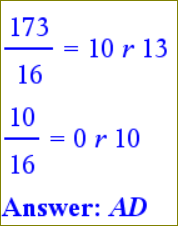Beginning from the right to left: number1 · 2^position(0)+number2 · 2^position(1)+…
So, beginning ALWAYS from the right and beginning ALWAYS counting from position ZERO, the first one is a 1, position 0, so it would be 1·2^0, the second one, is also a 1, position 1th, so 1·2^1, the third one is a zero, 2th position, so 0·2^2… and so on:
1·2^0+1·2^1+0·2^2+1·2^3+1·2^4+0·2^5+1·2^6 = 1·1+1·2+0·4+1·8+1·16+0·32+1·64=1+2+8+16+64
I don’t know if I have explained well enough … 
Ah I understand now so it will be raised to the position it is in starting right to left at position 0. Thank you!
I went with 173 decimal and got 10101101 for the binary representation and AD for the hex representation.
To solve the hex, I began with convoluted arithmetic but about halfway through remembered something from my comp science classes decades ago. You can break the binary representation into chunks of four bits and then translate each bit to it’s hex representation. For example, 11110001 is F1 in hex. The first chunk of 4 bits, 1111, equals 15 decimal, or F hex. The second chunk, 0001, is 1 decimal, or 1 hex.
Great work @archbishopFPP.
Being able to break the binary string into bytes is one of the reasons hex is used a fair bit in computer science. They play very well together and hex is generally more human readable - especially when the binary string start getting longer.
For instance, if you had; 10110101100111011110
You could quickly break this down to 1011 (B) || 0101 (5) || 1001 (9) || 1101 (D) || 1110 (E) -> B59DE
Converting to decimal is still a bit of pain in either case but this trick for binary to hex conversion can be incredibly useful.
For 173:
Binary: 10101101
Hexadecimal: AD
For 34:
Binary: 100010
Hexadecimal: 22
For 173 :
bin
173/2 = 86 r 1
86/2 = 43 r 0
43/2 = 21 r 1
21 / 2 = 10 r 1
10 / 2 = 5 r 0
5 / 2 = 2 r 1
2/2 = 1 r 0
1/2 = 0 r 1
10101101
hexa
173/16 = 10 r 13
10/16 = 0 r 10
AD
For 42 :
42 / 2 = 21 r 0
21/ 2 = 10 r 1
10 / 2 = 5 r 0
5/2 = 2 r 1
2/2 = 1 r 0
1/2 = 0 r 1
101010
42 / 16 = 2 r 10
2 / 16 = 0 r 2
2A
For 173 I got
AD in hex --> ( 16 * 10 ) + 13
10101101 in binary —> 1+ 4+ 8+32 + 128
Then tried 289
121 in hex --> 16^2 +2(16^1) + 1(16^0) = 256 + 32 + 1
100100001 --> 1 + 32 + 256
The results I got for 173:
Hex: AD
Bin: 10101101
Also made a post here how I verified my results with code:
Number 723
In bin: 1011010011
In hex: 2D3
Challenge 173:
In bin:
173 / 2 = 86 r 1
56 / 2 = 43 r 0
43 / 2 = 21 r 1
21 / 2 = 10 r 1
10 / 2 = 5 r 0
5 / 2 = 2 r 1
2 / 2 = 1 r 0
1 / 2 = 0 r 1
10101101
In hex:
173 / 16 = 10 r 13
10 / 16 = 0 r 10
10 = A
13 = D
AD
New number:
number is 2046
In bin:
2046 / 2 = 1023 r 0
1023 / 2 = 511 r 1
511 / 2 = 255 r 1
255 / 2 = 127 r 1
127 / 2 = 63 r 1
63 / 2 = 31 r 1
31 / 2 = 15 r 1
15 / 2 = 7 r 1
7 / 2 = 3 r 1
3 / 2 = 1 r 1
1 / 2 = 0 r 1
11111111110
In hex:
2046 / 16 = 127 r 14
127 / 16 = 7 r 15
7 / 16 = 0 r 7
15 = F
14 = E
7FE
173:
Binary:
173 / 2 = 86 reminder 1
86 / 2 = 43 reminder 0
43 / 2 = 21 reminder 1
21 / 2 = 10 reminder 1
10 / 2 = 5 reminder 0
5 / 2 = 2 reminder 1
2 / 2 = 1 reminder 0
1 / 2 = 0 reminder 1
Binary = 10101101
Hex:
173 / 16 = 10 reminder 13
10 / 16 = 0 reminder 10
Hex = AD
398:
Binary:
398 / 2 = 199 reminder 0
199 / 2 = 99 reminder 1
99 / 2 = 49 reminder 1
49 / 2 = 24 reminder 1
24 / 2 = 12 reminder 0
12 / 2 = 6 reminder 0
6 / 2 = 3 reminder 0
3 / 2 = 1 reminder 1
1 / 2 = 0 reminder 1
Binary = 110001110
Hex:
398 / 16 = 24 reminder 14
24 / 16 = 1 reminder 8
1 / 16 = 0 reminder 1
Hex = 18E
I used the integer ‘69’ for this practice:
Binary Conversion:
69 / 2 = 34 r 1
34 / 2 = 17 r 0
17 / 2 = 8 r 1
8 / 2 = 4 r 0
4 / 2 = 2 r 0
2 / 2 = 1 r 0
1 / 2 = 0 r 1
69 = 1000101
Hexadecimal Conversion:
69 / 16 = 4 r 5
4 / 16 = 0 r 4
69 = 45
Here’s my attempt at the binary and hexadecimal conversions. I started with the given value of 173, and then did my own of 117:
173 Binary:
173 / 2 = 86 r 1
86 / 2 = 43 r 0
43 / 2 = 21 r 1
21 / 2 = 10 r 1
10 / 2 = 5 r 0
5 / 2 = 2 r 1
2 / 2 = 1 r 0
1 / 2 = 0 r 1
Binary Result: 10101101
173 Hexadecimal:
173 / 16 = 10 r 13
10 / 16 = 0 r 10
(In Hexadecimal: 13 = D, 10 = A)
Hexadecimal Result: AD
117 Binary:
117 / 2 = 58 r 1
58 / 2 = 29 r 0
29 / 2 = 14 r 1
14 / 2 = 7 r 0
7 / 2 = 3 r 1
3 / 2 = 1 r 1
1 / 2 = 0 r 1
Binary Result: 1110101
117 Hexadecimal:
117 / 16 = 7 r 5
7 / 16 = 0 r 7
Hexadecimal Result: 75
Here’s my solution for number 42
Binary
42/2 = 2 r 0
21/2 = 10 r 1
10/2 = 5 r 0
5/2 = 2 r 1
2/2 = 1 r 0
1/2 = 0 r 1
42 → 101010 in binary form
Hex solution
42/16 = 2 r A
2/16 = 0 r 2
42 → 2A in hex form
173 in binary:
173 / 2 =
86 r 1
43 r 0
21 r 1
10 r 1
5 r 0
2 r 1
1 r 0
0 r 1
So 173 in binary = 10101101
173 in hexadecimal:
173 / 16 =
10 r 13
0 r 10
So 173 in hexadecimal = AD
235 in binary:
235 / 2 =
117 r 1
58 r 1
29 r 0
14 r 1
7 r 0
3 r 1
1 r 1
0 r 1
So 235 in binary = 11101011
235 in hexadecimal:
235 / 16 =
14 r 11
0 r 14
So 235 in hexadecimal = EB
I chose 293.
Binary: 100100101
Hex: 125
In double-checking the Hex I forgot that for each place we multiple the previous by 16 (so the 3rd place is 256) so couldn’t figure out why I couldn’t re-convert it. Finally got it tho! This is fun stuff! I feel like I’m starting to get things that have long eluded me.
173 is
10101101
AD
my number is 420
110100100
44
I did the 173:
DEC → BINARY
173 ÷ 2 = 86 r 1
86 ÷ 2 = 43 r 0
43 ÷ 2 = 21 r 1
21 ÷ 2 = 10 r 1
10 ÷ 2 = 5 r 0
5 ÷ 2 = 2 r 1
2 ÷ 2 = 1 r 0
1 ÷ 2 = 0 r 1
Dec: 173
Binary: 10101101
Dec->Hex
173 ÷ 16 = 10 r 13 (D)
10 ÷ 16 = 0 r 10 (A)
Dec: 173
Hex: AD
