9 - 3 : (1/3) + 1 = x
- -3 : (1/3) = -3 * (3/1) = -9 => 9 - 9 + 1 = x
- 9 - 9 = 0 => 0 + 1 = x
- 0 + 1 = 1 => 1 = x
x = 1

9 - 3 : (1/3) + 1 = x
x = 1
I got -1, using PEMDAS, which I learned in school way back when.
Parentheses, Exponents, Multiply, Divide, Add, Subract
To wit: 9 - 3 / 1/3 + 1
First divide 3 by 1/3, which is the same as multiplying it by 3, which gives you 9, so:
9 - 9 + 1
In PEMDAS, Add comes before Subtract, so you get:
9 - 10 = -1
But like Rick said in the video, we don’t have enough information. From these last couple of lessons, it’s clicked intuitively for me that multiplication is the same as repeated addition, and division is the same as repeated subtraction.
So I think that explains why you would multiply and divide before adding and subtracting, and also why you would do the parentheses (brackets) first.
Parentheses: Explicit groupings of values-- (3 x 2) / 3 = 2
Exponents: Repeated multiplication
Multiplication: Repeated Addition
Division: Repeated Subtraction
Addition
Subtraction
So it makes sense that you would first follow the instructions for grouping values, then perform the repeated operations before the individual ones. But I’m less clear on why multiplication precedes division, and by extension, why addition precedes subtraction.
Any math whizzes want to explain this to me? Is it just a convention, or is there a “natural”, intuitive reason we add before we subtract?
When applying PEMDAS, multiplication and division have the same precedence as each other, as do addition and subtraction.
This means that when these operations are next to each other, you solve them from left to right.
One way to look at subtraction is a the addition of a negative number.
So instead of 9 - 9 + 1, you could rewrite this as 9 + (-9) + 1, so this should always evaluate to 1.
And for division, you can view that as multiplying by the reciprocal of a number, rather than as repeated subtraction. This just means that you flip the fraction.
So 3 / (1/3) is the same as 3 * (3/1).
So this gives you;
9 - 3 / (1/3) + 1
9 + (-3) * 3 + 1
9 + (- 9) + 1
1
I hope that explanation helps.
Ah, that makes sense. Thanks!
I used the browser console and ran this through JavaScript and when converting the fraction to a decimal, you get the same result w/o parentheses because the math is calculated in the correct order:
9 - 3 ÷ .333 + 1 = ?
let nine = 9;
let three = 3;
let onethird = 0.333;
let one = 1;
nine - (three / onethird) + one = 0.9909909909909906
nine - three /onethird + one = 0.9909909909909906
The way I was taught, and retaught on khan academy was the division would come first
3 / (1 / 3)
(3 / 1) / (1 / 3)
3 / 3
= 1
thus
9 - 1 + 1 = 9
Hi Matt, you made a slight error in your calculation there.
(3/1) / (1/3) = 9
It would only equal 1 if you did (3/1) x (1/3), but that would require changing the operator without adjusting your fractions accordingly.
If you want to change the operator from a division to a multiplication then you also have to flip the fraction.
So you’d get;
(3/1) x (3/1) = 9/1 = 9
The way to make it 9 would be to do (3/1) / 3, rather than 3 / (1/3), but the way the question is presented implies that it’s the latter due to the use of the ÷ symbol and displaying 1/3 as a proper fraction.
Since I basically remember nothing about order of operations, aside from there is one, I just made a guess. Winging it I came up with two possible answers 4.5 and 19. Looking here at the discussion on the solution I can see how you all came to the answer of 1. Although, I wonder if given a similar problem if I would be able to identify that I should be adding a negative and multiplying a inverse.
Here’s what I did to get my incorrect numbers. 6 ÷ 1.33333 = 4.5 and 6 ÷ .33333 + 1 = 19
posting for others in my situation, so they don’t feel alone.
Thanks a lot for sharing your solution. 
I’m sure if you take another look at the BODMAS mnemotic (or an equivalent) and try the challenge again, you’ll remember the correct order and get the correct result. Unfortunately, the correct order is crucial to get the correct result in maths. For this reason, it’s advisable to learn this. Maybe you could print out a diagram or make a sketch which you could pin to your wall near your desk.
If I solved it using Ben’s equation from the lecture (where 1/3 is clearly a fraction) my answer would be 1.
If I solved it using the title of this post (which makes no distinction between division and fractions) my answer would be 9.
The title might be better represented to make fraction precedence clear (lacking the ability to write fractions on this platform):
9 - 3 / (1 / 3) + 1 = ?
Python:
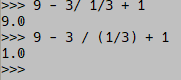
Unless the whole point was to be ambiguous, in which case, carry on…
I also got 1 (as written in the video the way I would translate that here would be (via PEMDAS L to R) since 1/3 was written as a fraction (top over bottom) instead of 1/3 which would indicate division. However, point taken regarding confusion based on notation.
9 - 3 / (1/3) +1
9 - 9 + 1
0 + 1
1
9 - ( 3 / ( 1 / 3 ) ) +1 = 1
Following Order of operations Start with
3 ÷ 1/3
Turn the 1/3 upside down and multiply
3×3/1=9
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Putting it all back together
9−9=0
0+1=1
Hi
I got 1, made me think alot about it.
But first I got 11, but that had to be wrong, then I understod. It’s been a while , it’s so good to go back to basics.
Absolutly love this course.
My first answer was 7, then I realized I read it as “-3 multiplied by 1/3” instead of “-3 divided by 1/3”! My answer is 1.
that is correct
9 - ( 3 / (1/3)) + 1
9 - (9) + 1 = 1
Yep, I got the same with some quick head math.